题目内容
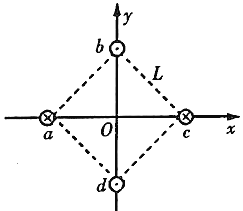
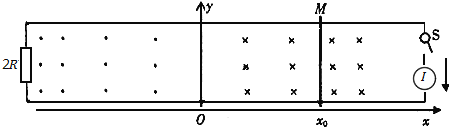
【题目】间距为L的两平行光滑金属导轨如图所示,x轴平行导轨,y轴垂直导轨。在y轴位置有一厚度可不计的绝缘层,隔开左右两部分电路。在导轨间存在的磁场,y轴左侧磁场方向垂直纸面向里,y轴右侧磁场方向垂直纸面向外,y轴左右两侧的磁感应强度大小相对y轴对称,且沿y轴方向磁感应强度大小不变,沿x轴方向磁感应强度大小随x变化,在x=x0处磁感应强度大小为B0,导轨右侧的恒流源为电路提供恒定的电流I,开关S接通时,电流方向如图所示,导轨左侧接一阻值为2R的电阻。有一阻值为R的金属棒M垂直导轨静止置于x=x0处,当开关S接通时发现其在y轴右侧的位移随时间的变化规律为x=x0cosωt,其中ω为常数。金属棒在y轴左侧导轨运动的最大距离为xm(xm<x0),求:
(1)磁感应强度大小B与x的函数关系;
(2)开关S接通到金属棒运动至y轴左侧最远处的过程中流过金属棒的电量q;
(3)在y轴左侧运动时,金属棒产生的焦耳热Q。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)金属棒做简谐运动,则有
F=-kx=-BIL
当x=x0时
![]()
解得
![]()
(2)从x0运动到0的过程中,流过的电量
![]()
从0运动到左边最远处的过程中,流过的电量
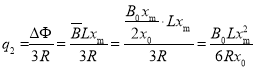
整个过程的电量为
![]()
(3)从x0运动到0的过程中,由动能定理
![]()
![]()
从0运动到左边最远处的过程中,由能量守恒可得金属棒产生的焦耳热Q,则
![]()

练习册系列答案
相关题目