题目内容
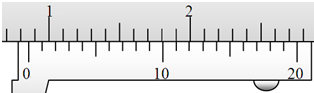 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d(读数如图).
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d(读数如图).(1)该单摆在摆动过程中的周期为
| 2t |
| n-1 |
| 2t |
| n-1 |
(2)用上述物理量的符号写出求重力加速度的一般表达式g=
| π2(n-1)2(2L+d) |
| 2t2 |
| π2(n-1)2(2L+d) |
| 2t2 |
(3)从图可知,摆球的直径为
8.55
8.55
mm.(4)实验结束后,某同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中的
BD
BD
.A.单摆的悬点未固定紧,振动中出现松动,使摆线增长了
B.把n次摆动的时间误记为(n+1)次摆动的时间
C.以摆线长作为摆长来计算
D.以摆线长与摆球的直径之和作为摆长来计算.
分析:(1)根据从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t,确定单摆全振动的次数,再求解周期.
(2)单摆的长度为l=L+
.将摆长、周期代入单摆的周期公式求出重力加速度的表达式g.
(3)游标卡尺读数等于固定刻度读数加游标尺读数,不需要估读;
(4)对于测量误差可根据实验原理进行分析.
(2)单摆的长度为l=L+
| d |
| 2 |
(3)游标卡尺读数等于固定刻度读数加游标尺读数,不需要估读;
(4)对于测量误差可根据实验原理进行分析.
解答:解:(1)由题,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t,则单摆全振动的次数为N=
,
周期T=
=
(2)单摆的长度为l=L+
.由单摆的周期公式T=2π
得,g=
.
将为l=L+
,T=
代入解得g=
(3)游标卡尺读数等于固定刻度读数加游标尺读数;
固定刻度读数为:8mm;
游标尺第11刻线与主尺刻线对其,读数为0.55mm,故读数为:8.55 mm
(4)A、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,测得的单摆周期变大,根据g=
可知,测得的g应偏小.故A错误;
B、实验中误将n次全振动计为n+1次,根据T=
求出的周期变小,g偏大.故B正确;
C、以摆线长作为摆长来计算,摆长偏小,根据g=
可知,测得的g应偏小.故C错误;
D、以摆线长与摆球的直径之和作为摆长来计算,摆长偏大,根据g=
可知,测得的g应偏大.故D正确.
故选BD;
故答案为:
(1)
(2)
(3)8.55 (4)BD
| n-1 |
| 2 |
周期T=
| t |
| N |
| 2t |
| n-1 |
(2)单摆的长度为l=L+
| d |
| 2 |
|
| 4π2l |
| T2 |
将为l=L+
| d |
| 2 |
| 2t |
| n-1 |
代入解得g=
| π2(n-1)2(2L+d) |
| 2t2 |
(3)游标卡尺读数等于固定刻度读数加游标尺读数;
固定刻度读数为:8mm;
游标尺第11刻线与主尺刻线对其,读数为0.55mm,故读数为:8.55 mm
(4)A、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,测得的单摆周期变大,根据g=
| 4π2l |
| T2 |
B、实验中误将n次全振动计为n+1次,根据T=
| t |
| n |
C、以摆线长作为摆长来计算,摆长偏小,根据g=
| 4π2l |
| T2 |
D、以摆线长与摆球的直径之和作为摆长来计算,摆长偏大,根据g=
| 4π2l |
| T2 |
故选BD;
故答案为:
(1)
| 2t |
| n-1 |
| π2(n-1)2(2L+d) |
| 2t2 |
点评:常用仪器的读数要掌握,这是物理实验的基础.掌握单摆的周期公式,从而求解加速度,摆长、周期等物理量之间的关系.单摆的周期采用累积法测量可减小误差.对于测量误差可根据实验原理进行分析.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.
某实验小组在进行“用单摆测定重力加速度”的实验中,已知单摆在摆动过程中的摆角小于5°;在测量单摆的周期时,从单摆运动到最低点开始计时且记数为1,到第n次经过最低点所用的时间内为t;在测量单摆的摆长时,先用毫米刻度尺测得悬挂后的摆线长(从悬点到摆球的最上端)为L,再用游标卡尺测得摆球的直径为d.