题目内容
7. 在做“研究平抛运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口的方向平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;将木板再向远离槽口的方向平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)
在做“研究平抛运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口的方向平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;将木板再向远离槽口的方向平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)(1)为什么每次都要使小球从斜槽上紧靠挡板处由静止释放?为了保证小球每次做平抛运动的初速度相同.
(2)根据以上直接测量的物理量来求得小球初速度的表达式为v0=x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$.(用题中所给字母表示)
(3)小球初速度的值为v0=1.00m/s.
分析 明确实验的注意事项,根据平抛运动规律在水平和竖直方向的规律,尤其是在竖直方向上,连续相等时间内的位移差为常数,列出方程即可正确求解.
解答 解:(1)该实验中,为了确保小球每次抛出的轨迹相同,应该使抛出时的初速度相同,因此每次都应使小球从斜槽上紧靠档板处由静止释放.
(2)在竖直方向上:△y=y2-y1=gt2
水平方向上:x=v0t
联立方程解得:v0=x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$.
(3)根据:v0=x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$ 代入数据解得:v0=1.00m/s
故答案为:(1)为了保证小球每次做平抛运动的初速度相同;(2)x$\sqrt{\frac{g}{{y}_{2}-{y}_{1}}}$;(3)1.00.
点评 本题主要考查了匀变速直线运动中基本规律以及推论的应用,平时要加强练习,提高应用基本规律解决问题能力.

练习册系列答案
相关题目
18.下列对电现象及规律的认识中,正确的是( )
| A. | 摩擦起电说明了电荷可以创生 | |
| B. | 点电荷间的静电力随它们的距离增大而增大 | |
| C. | 同种电荷相互排斥,异种电荷相互吸引 | |
| D. | 自由电子带正电,质子带负电 |
19. 物块从光滑曲面上由P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带以一定的速度运动,如图所示,再把物块放到P点自由滑下,则( )
物块从光滑曲面上由P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带以一定的速度运动,如图所示,再把物块放到P点自由滑下,则( )
 物块从光滑曲面上由P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带以一定的速度运动,如图所示,再把物块放到P点自由滑下,则( )
物块从光滑曲面上由P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带以一定的速度运动,如图所示,再把物块放到P点自由滑下,则( )| A. | 若传送带逆时针运动,物块可能返回曲面 | |
| B. | 若传送带逆时针运动,物块将仍然落在Q点 | |
| C. | 若传送带顺时针运动,物块可能落在Q点左边 | |
| D. | 若传送带顺时针运动,物块可能落在Q点右边 |
11.以初速度v0水平抛出一物体,当物体的水平位移是竖直位移的2倍时,物体的竖直分速度大小为( )
| A. | $\frac{{v}_{0}}{2}$ | B. | v0 | C. | 2v0 | D. | 4v0 |
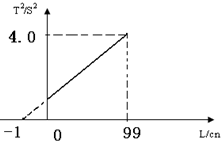 某同学在做“用单摆测定重力加速度”的实验时,为求出当地的重力加速度,根据实验数据作出了T2-L图象,如图所示.
某同学在做“用单摆测定重力加速度”的实验时,为求出当地的重力加速度,根据实验数据作出了T2-L图象,如图所示.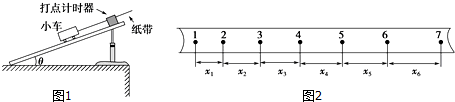
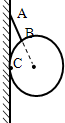 如图所示,竖直墙上A点用AB细线悬挂一个光滑小球,小球质量为m=3kg,半径r=0.3m,细线AB长L=0.2m,C为接触点,求AB绳和墙在C点对球的作用力分别为多大?
如图所示,竖直墙上A点用AB细线悬挂一个光滑小球,小球质量为m=3kg,半径r=0.3m,细线AB长L=0.2m,C为接触点,求AB绳和墙在C点对球的作用力分别为多大?