题目内容
15.某实验小组测量小车从斜面上下滑所受到的阻力大小,实验装置如图1所示,一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下.图2是打出的纸带的一段,已量出各相邻计数点(相邻计数点间还有4个点未画出)的长度分别为:x1、x2、x3、x4、x5、x6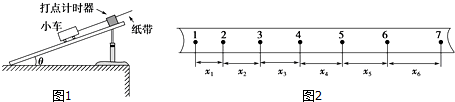
(1)已知打点计时器使用的交流电频率为f,则打下3计数点时小车的速度v3=$\frac{{x}_{2}+{x}_{3}}{10}f$,小车下滑的加速度算式为a=$\frac{[({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})]{f}^{2}}{225}$(用题中所给的符号表示).
(2)已知当地的重力加速度为g,本实验中只有毫米刻度尺,没有量角器,为了求出小车在下滑过程中所受的阻力,还需测量的物理量有小车质量m、斜面上任意两点间距离l及这两点的高度差h (要用文字及符号表示).
(3)用加速度a及其他需要测得的量表示阻力的计算式为F阻=mg$\frac{h}{l}$-ma.
分析 (1)匀变速直线运动中,平均速度等于中间时刻的瞬时速度,根据△x=aT2列式求解加速度;
(2、3)根据牛顿第二定律列式求解阻力,确定待测量.
解答 解:(1)相邻计数点间还有4个点未画出,打点计时器使用的交流电频率为f,则$T=5\frac{1}{f}=\frac{5}{f}$
匀变速直线运动中,平均速度等于中间时刻的瞬时速度,故:
V3=$\frac{{x}_{24}}{2T}=\frac{{x}_{2}+{x}_{3}}{10}f$
根据公式△x=aT2,有:
(x6+x5+x4)-(x1+x2+x3)=a(3T)2
解得:
a=$\frac{[({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})]{f}^{2}}{225}$,
(2、3)根据牛顿第二定律,有:
mgsinθ-F阻=ma
解得:
F阻=mgsinθ-ma=mg$\frac{h}{l}$-ma
故还需要测量小车质量m、斜面上任意两点间距离l及这两点的高度差h;
故答案为:(1)$\frac{{x}_{24}}{2T}=\frac{{x}_{2}+{x}_{3}}{10}f$;$\frac{[({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})]{f}^{2}}{225}$;
(2)小车质量m; 斜面上任意两点间距离l及这两点的高度差h;
(3)mg$\frac{h}{l}$-ma
点评 本题关键是明确小车的受力情况和运动性质,然后结合运动学公式和牛顿第二定律定律列式求解.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
6.下列说法正确的是( )
| A. | 硬币或钢针能浮于水面上,是由于液体表面张力的作用 | |
| B. | 晶体有固定的熔点,具有规则的几何外形,物理性质具有各向异性 | |
| C. | 布朗运动反映了液体分子是在做永不停息无规则热运动 | |
| D. | 可以将散失在环境中的内能重新收集起来加以利用而不引起其他变化 |
10. 2009年诺贝尔物理学奖得主威拉德•博伊尔和乔治•史密斯主要成就是发明了电荷耦合器件(CCD)图象传感器.他们的发明利用了爱因斯坦的光电效应原理.如图所示电路可研究光电效应规律.图中标有A和K的为光电管,其中K为阴极,A为阳极.理想电流计可检测通过光电管的电流,理想电压表用来指示光电管两端的电压.现接通电源,用光子能量为10.5eV的光照射阴极K,电流计中有示数,若将滑动变阻器的滑片P缓慢向右滑动,电流计的读数逐渐减小,当滑至某一位置时电流计的读数恰好为零,读出此时电压表的示数
2009年诺贝尔物理学奖得主威拉德•博伊尔和乔治•史密斯主要成就是发明了电荷耦合器件(CCD)图象传感器.他们的发明利用了爱因斯坦的光电效应原理.如图所示电路可研究光电效应规律.图中标有A和K的为光电管,其中K为阴极,A为阳极.理想电流计可检测通过光电管的电流,理想电压表用来指示光电管两端的电压.现接通电源,用光子能量为10.5eV的光照射阴极K,电流计中有示数,若将滑动变阻器的滑片P缓慢向右滑动,电流计的读数逐渐减小,当滑至某一位置时电流计的读数恰好为零,读出此时电压表的示数
为6.0V;现保持滑片P位置不变,以下判断正确的是( )
 2009年诺贝尔物理学奖得主威拉德•博伊尔和乔治•史密斯主要成就是发明了电荷耦合器件(CCD)图象传感器.他们的发明利用了爱因斯坦的光电效应原理.如图所示电路可研究光电效应规律.图中标有A和K的为光电管,其中K为阴极,A为阳极.理想电流计可检测通过光电管的电流,理想电压表用来指示光电管两端的电压.现接通电源,用光子能量为10.5eV的光照射阴极K,电流计中有示数,若将滑动变阻器的滑片P缓慢向右滑动,电流计的读数逐渐减小,当滑至某一位置时电流计的读数恰好为零,读出此时电压表的示数
2009年诺贝尔物理学奖得主威拉德•博伊尔和乔治•史密斯主要成就是发明了电荷耦合器件(CCD)图象传感器.他们的发明利用了爱因斯坦的光电效应原理.如图所示电路可研究光电效应规律.图中标有A和K的为光电管,其中K为阴极,A为阳极.理想电流计可检测通过光电管的电流,理想电压表用来指示光电管两端的电压.现接通电源,用光子能量为10.5eV的光照射阴极K,电流计中有示数,若将滑动变阻器的滑片P缓慢向右滑动,电流计的读数逐渐减小,当滑至某一位置时电流计的读数恰好为零,读出此时电压表的示数为6.0V;现保持滑片P位置不变,以下判断正确的是( )
| A. | 光电管阴极材料的逸出功为4.5eV | |
| B. | 若增大入射光的强度,电流计的读数不为零 | |
| C. | 若用光子能量为12eV的光照射阴极K,光电子的最大初动能一定变大 | |
| D. | 若用光子能量为9.5eV的光照射阴极K,同时把滑片P向左移动少许,电流计的读数一定不为零 |
20. 如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )
如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )
 如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )
如图所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m则以下说法正确的是( )| A. | 小球沿三种不同轨道下滑到桌面上的过程,重力做功一样多 | |
| B. | 小球沿曲线轨道下滑到桌面上的过程,重力做功最多 | |
| C. | 以桌面为参考面,小球的重力势能的减少量为mgh | |
| D. | 以地面为参考面,小球的重力势能的减少量为mg(H+h) |
19.下列说法正确的是( )
| A. | 电场中电场线一定是直线 | |
| B. | 电势差的大小与零电势点的选取有关 | |
| C. | 电场中电势高的地方电势能越高 | |
| D. | 电场线方向与等势面处处相垂直 |
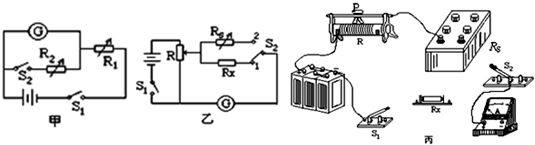
 在做“研究平抛运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口的方向平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;将木板再向远离槽口的方向平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)
在做“研究平抛运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口的方向平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;将木板再向远离槽口的方向平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2) 如图所示的曲线表示某一电场的电场线(未表明方向),把一带电荷量为2×10-8C的正点电荷从A点移至B点时,电场力做了6×10-4J的功,且在B点受到电场力为4×10-6N,试求:
如图所示的曲线表示某一电场的电场线(未表明方向),把一带电荷量为2×10-8C的正点电荷从A点移至B点时,电场力做了6×10-4J的功,且在B点受到电场力为4×10-6N,试求: