题目内容
6. 如图所示,木块A静止在斜面体B上.设木块受到斜面体的支持力大小为N,摩擦力大小为f.当斜面体水平向左做加速度逐渐增大的加速运动时,若木块A相对于斜面体B始终保持
如图所示,木块A静止在斜面体B上.设木块受到斜面体的支持力大小为N,摩擦力大小为f.当斜面体水平向左做加速度逐渐增大的加速运动时,若木块A相对于斜面体B始终保持静止,则( )
| A. | N增大,f增大 | B. | N不变,f增大 | ||
| C. | N减小,f先增大后减小 | D. | N增大,f先减小后增大 |
分析 使物体和斜面体一起向左做加速运动,加速度水平向左,将加速度分解为沿斜面向下和垂直于斜面向上两个方向,根据牛顿第二定律得到支持力N和摩擦力f的关系式进行分析.
解答 解:当加速度较小时,摩擦力f沿斜面向上.将加速度分解为沿斜面向下和垂直于斜面向上.根据牛顿第二定律得
N-mgcosθ=masinθ,
mgsinθ-f=macosθ,
得到N=mgcosθ+masinθ;
f=mgsinθ-macosθ
可知当a增大时,N增大,f减小.
当加速度较大时,摩擦力f沿斜面向下.根据牛顿第二定律得
N-mgcosθ=masinθ,
mgsinθ+f=macosθ,
得到N-mgcosθ=masinθ,f=macosθ-mgsinθ
可知当a增大时,N增大,f增大.
所以N增大,f先减小后增大.故 D正确,A、B、C错误.
故选:D.
点评 本题考查灵活运用正交分解处理物理问题的能力,采用的是分解加速度,不分解要求的力的方法,使解题过程简洁方便.

练习册系列答案
相关题目
17.恒星的前身是( )
| A. | 宇宙的微粒 | B. | 星团 | ||
| C. | 行星 | D. | 星际云或星际云中的某块星云 |
14. 固定的光滑导轨间距为L,阻值为R的电阻,夹角为θ,磁感应强度大小为B、质量为m、电阻为r的导体棒,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行,则( )
固定的光滑导轨间距为L,阻值为R的电阻,夹角为θ,磁感应强度大小为B、质量为m、电阻为r的导体棒,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行,则( )
 固定的光滑导轨间距为L,阻值为R的电阻,夹角为θ,磁感应强度大小为B、质量为m、电阻为r的导体棒,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行,则( )
固定的光滑导轨间距为L,阻值为R的电阻,夹角为θ,磁感应强度大小为B、质量为m、电阻为r的导体棒,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行,则( )| A. | 初始时刻通过电阻R的电流I的大小I1=$\frac{BL{v}_{0}}{(R+r)}$,电流方向为a→b | |
| B. | 当导体棒第一次回到初始位置时,速度变为v,此时导体棒的加速度大小a=gsinθ-$\frac{{B}^{2}{L}^{2}v}{m(R+r)}$ | |
| C. | 导体棒最终静止时弹簧的弹性势能为Ep,求导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热 Q=$\frac{R}{R+r}$[$\frac{1}{2}$mv02+$\frac{(mgsinθ)^{2}}{k}$-Ep] | |
| D. | .导体棒最终静止时弹簧的弹性势能为Ep,求导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热 Q=[$\frac{1}{2}$mv02+$\frac{(mgsinθ)^{2}}{k}$-Ep] |
1.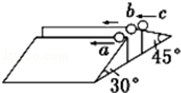 如图所示,两个倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等.有三个完全相同的小球a、b、c,开始均静止于同一高度处,其中b小球在两斜面之间,a、c两小球在斜面顶端.若同时沿水平方向抛出,初速度方向如图所示,小球a、b、c到达该水平面的时间分别为t1、t2、t3.下列关于时间的关系正确的是( )
如图所示,两个倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等.有三个完全相同的小球a、b、c,开始均静止于同一高度处,其中b小球在两斜面之间,a、c两小球在斜面顶端.若同时沿水平方向抛出,初速度方向如图所示,小球a、b、c到达该水平面的时间分别为t1、t2、t3.下列关于时间的关系正确的是( )
 如图所示,两个倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等.有三个完全相同的小球a、b、c,开始均静止于同一高度处,其中b小球在两斜面之间,a、c两小球在斜面顶端.若同时沿水平方向抛出,初速度方向如图所示,小球a、b、c到达该水平面的时间分别为t1、t2、t3.下列关于时间的关系正确的是( )
如图所示,两个倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等.有三个完全相同的小球a、b、c,开始均静止于同一高度处,其中b小球在两斜面之间,a、c两小球在斜面顶端.若同时沿水平方向抛出,初速度方向如图所示,小球a、b、c到达该水平面的时间分别为t1、t2、t3.下列关于时间的关系正确的是( )| A. | t1>t2>t3 | B. | t1>t3>t2 | C. | t1<t3<t2 | D. | t1<t2<t3 |
11. 如图所示,AB杆以恒定角速度绕A点转动,并带动套在水平杆OC上的质量为M的小环运动,运动开始时,AB杆在竖直位置,则小环M的加速度将( )
如图所示,AB杆以恒定角速度绕A点转动,并带动套在水平杆OC上的质量为M的小环运动,运动开始时,AB杆在竖直位置,则小环M的加速度将( )
 如图所示,AB杆以恒定角速度绕A点转动,并带动套在水平杆OC上的质量为M的小环运动,运动开始时,AB杆在竖直位置,则小环M的加速度将( )
如图所示,AB杆以恒定角速度绕A点转动,并带动套在水平杆OC上的质量为M的小环运动,运动开始时,AB杆在竖直位置,则小环M的加速度将( )| A. | 逐渐增大 | B. | 先减小后增大 | C. | 先增大后减小 | D. | 逐渐减小 |
15. 如图所示,A,B,C,D为四个完全相同的光滑圆柱体,质量均为m,两块相同的光滑竖直挡板在大小相等的水平推力F作用下使四个圆柱体处于静止状态,如图所示已知当地的重力加速度为g,则有( )
如图所示,A,B,C,D为四个完全相同的光滑圆柱体,质量均为m,两块相同的光滑竖直挡板在大小相等的水平推力F作用下使四个圆柱体处于静止状态,如图所示已知当地的重力加速度为g,则有( )
 如图所示,A,B,C,D为四个完全相同的光滑圆柱体,质量均为m,两块相同的光滑竖直挡板在大小相等的水平推力F作用下使四个圆柱体处于静止状态,如图所示已知当地的重力加速度为g,则有( )
如图所示,A,B,C,D为四个完全相同的光滑圆柱体,质量均为m,两块相同的光滑竖直挡板在大小相等的水平推力F作用下使四个圆柱体处于静止状态,如图所示已知当地的重力加速度为g,则有( )| A. | 力F的最小值为$\sqrt{3}$mg | B. | 力F的最大值为$\sqrt{3}$mg | ||
| C. | B球对A球的弹力大小等于mg | D. | 若减小F,则B和A之间的弹力增加 |
16.二十世纪初,为研究物质的内部结构,物理学家做了大量的实验,如图装置的实验是( )

| A. | α粒子散射实验 | B. | 发现质子的实验 | C. | 发现电子的实验 | D. | 发现中子的实验 |

 如图所示,abcd为用粗细均匀的同种材料制成的金属线框,其中ab的长度只有bc长度的一半.现将线框放在水平光滑绝缘的桌面上,在外力F的作用下让线框以速度v匀速穿过右边两个磁感应强度大小相等、方向相反的磁场区域.若以图示位置开始计时,规定逆时针电流方向为正,磁感线向下穿过线框时的磁通量为正.则下列关于回路电流i、外力F大小、c b间的电势差Ucb及穿过线框的磁通量φ随时间变化的图象正确的是( )
如图所示,abcd为用粗细均匀的同种材料制成的金属线框,其中ab的长度只有bc长度的一半.现将线框放在水平光滑绝缘的桌面上,在外力F的作用下让线框以速度v匀速穿过右边两个磁感应强度大小相等、方向相反的磁场区域.若以图示位置开始计时,规定逆时针电流方向为正,磁感线向下穿过线框时的磁通量为正.则下列关于回路电流i、外力F大小、c b间的电势差Ucb及穿过线框的磁通量φ随时间变化的图象正确的是( )


