题目内容
18.在一次警车A追击劫匪车B时,两车同时由静止向同一方向加速行驶,经过30s追上.两车各自的加速度为aA=15m/s2,aB=10m/s2,各车最高时速分别为vA=45m/s,vB=40m/s,(1)警车A加速运动的时间t1
(2)警车A加速阶段的位移L1及匀速阶段的位移L2
(3)两车原来相距多远?
分析 (1)根据速度时间公式求出警车A加速运动的时间.
(2)根据位移时间公式求出警车加速阶段的位移,通过匀速运动的时间求出匀速运动的位移.
(3)根据两者的位移关系,结合运动学公式求出两车原来相距的距离.
解答 解:(1)由vA=aA t1,解得t1=$\frac{{v}_{A}}{{a}_{A}}=\frac{45}{15}s$=3 s
匀速运动的时间t2=30-3s=27 s,
(2)警车在0~3 s时间段内做匀加速运动,
L1=$\frac{1}{2}$aA t12=$\frac{1}{2}×15×9m$=67.5m
在3~30 s时间段内做匀速运动,则L2=vAt2=45×27m=1215m.
(3)警车追上劫匪车的全部行程为
L=L1+L2=$\frac{1}{2}$aA t12+vA t2=67.5+1215=1 282.5 m
同理tB1=4 s,tB2=26 s
同理劫匪车被追上时的全部行程为
l=l1+l2=$\frac{1}{2}$aB tB12+vB tB2
代入数据解得l=1 120 m,
两车原来相距△L=L-l=162.5 m.
答:(1)警车A加速运动的时间为3s;
(2)警车A加速阶段的位移为67.5m,匀速阶段的位移为1215m;
(3)两车原来相距162.5 m.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,掌握匀变速直线运动的速度时间公式、位移时间公式是解决本题的关键.

练习册系列答案
相关题目
6.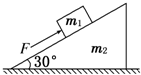 如图,用一平行于斜面的力F推滑块,使滑块静止于粗糙的斜面上,现增大力F,滑块和斜面体始终静止,则( )
如图,用一平行于斜面的力F推滑块,使滑块静止于粗糙的斜面上,现增大力F,滑块和斜面体始终静止,则( )
 如图,用一平行于斜面的力F推滑块,使滑块静止于粗糙的斜面上,现增大力F,滑块和斜面体始终静止,则( )
如图,用一平行于斜面的力F推滑块,使滑块静止于粗糙的斜面上,现增大力F,滑块和斜面体始终静止,则( )| A. | 斜面对滑块的摩擦力一定增大 | B. | 斜面对滑块的摩擦力可能不变 | ||
| C. | 地面对斜面体的摩擦力增大 | D. | 地面对斜面体的支持力增大 |
3.下面说法正确的是( )
| A. | 无卢瑟福依据α粒子散射实验的现象提出了原子的“核式结构”理论 | |
| B. | ${\;}_{1}^{1}$H+${\;}_{1}^{2}$H→${\;}_{2}^{2}$He+y是核聚变反应方程 | |
| C. | β射线是由原子核外的电子电离产生 | |
| D. | α射线是由氢原子核衰变产生 | |
| E. | 通过化学反应不能改变放射性物质的半衰期 |
7.将质量为0.5kg的小球以20m/s的初速度竖直向上抛出.不计空气阻力,g取10m/s2.以下判断正确的是( )
| A. | 小球从抛出至最高点受到的冲量大小为10 N•s | |
| B. | 小球从抛出至落回出发点动量的改变量大小为20 kgm/s | |
| C. | 小球从抛出至落回出发点受到的冲量大小为0 | |
| D. | 小球从抛出至落回出发点受到的冲量大小为20 N•s |
 如图所示,我国第一艘航母”辽宁号“上的舰载机歼-15在起飞过程中,某时刻的速度为250km/h.已知飞机竖直上升的分速度是150km/h,试求其水平方向的分速度和飞机与水平方向的夹角(已经sin37°=0.6,cos37°=0.8)
如图所示,我国第一艘航母”辽宁号“上的舰载机歼-15在起飞过程中,某时刻的速度为250km/h.已知飞机竖直上升的分速度是150km/h,试求其水平方向的分速度和飞机与水平方向的夹角(已经sin37°=0.6,cos37°=0.8)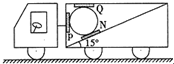 如图是汽车运送圆柱形工件的示意图,图中P、Q、N是固定在车体上的压力传感器,假设圆柱形工件表面光滑,汽车静止不动时Q传感器示数为零,P、N传感器示数不为零.当汽车向左匀加速启动过程中,P传感器示数为零而Q、N传感器示数不为零.已知sin15°=0.26,cos15°=0.97,tan15°=0.27,g=10m/s2.则汽车向左匀加速启动的加速度可能为( )
如图是汽车运送圆柱形工件的示意图,图中P、Q、N是固定在车体上的压力传感器,假设圆柱形工件表面光滑,汽车静止不动时Q传感器示数为零,P、N传感器示数不为零.当汽车向左匀加速启动过程中,P传感器示数为零而Q、N传感器示数不为零.已知sin15°=0.26,cos15°=0.97,tan15°=0.27,g=10m/s2.则汽车向左匀加速启动的加速度可能为( )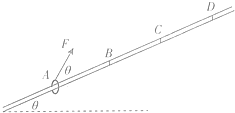 如图所示,一固定倾斜放置的粗糙直杆方向与水平方向的夹角为θ=37°,其上套有一质量为m的环,给环一个初速度让环沿杆下滑,环恰好能匀速下滑,现给环一斜向上的拉力,方向与杆的夹角也为θ,使环从A点由静止沿杆向上做匀加速直线运动,至C点时撤去拉力,结果环恰好能滑到D点,已知AB=BC=CD=L,重力加速度为g,拉力作用在环上时,杆对环的弹力垂直于杆向下,(已知sin 37°=0.6,cos 37°=0.8)求:
如图所示,一固定倾斜放置的粗糙直杆方向与水平方向的夹角为θ=37°,其上套有一质量为m的环,给环一个初速度让环沿杆下滑,环恰好能匀速下滑,现给环一斜向上的拉力,方向与杆的夹角也为θ,使环从A点由静止沿杆向上做匀加速直线运动,至C点时撤去拉力,结果环恰好能滑到D点,已知AB=BC=CD=L,重力加速度为g,拉力作用在环上时,杆对环的弹力垂直于杆向下,(已知sin 37°=0.6,cos 37°=0.8)求: 如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω;电阻R1=R2=R3=R4=3.0Ω;电容器的电容C=100μF.求电源的路端电压和电容器所带的电量.
如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω;电阻R1=R2=R3=R4=3.0Ω;电容器的电容C=100μF.求电源的路端电压和电容器所带的电量.