题目内容
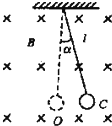在磁感应强度为B的匀强磁场中有一个单摆，如图所示，摆球的质量为m，带电荷量为+q，摆线长为L．当摆角α＜5°时，从C点由静止开始释放，那么在摆动过程中（ ）
| A、该单摆的周期T与磁感应强度及摆球带电荷量q有关 | B、摆球在最低点时，绳子的张力一定比在C点时的张力大 | C、摆球在最低点O的速度不为零，但加速度可能为零 | D、若不计空气阻力，摆球的机械能仍守恒 |
分析：带电的小球在磁场中受到洛伦兹力的作用，而洛伦兹力不做功，方向总与速度垂直，根据单摆的周期公式T=2π
分析周期．
分析小球在最低点时的受力，运用牛顿第二定律分析加速度．根据机械能守恒条件：只有重力做功，分析小球的机械能是否守恒．
|
分析小球在最低点时的受力，运用牛顿第二定律分析加速度．根据机械能守恒条件：只有重力做功，分析小球的机械能是否守恒．
解答：解：A、带电的小球在磁场中受到洛伦兹力的作用，而洛伦兹力不做功，方向总与速度垂直，不改变小球的速度大小即不改变小球的运动快慢，所以小球的摆动周期与磁场时相同，根据单摆的周期公式T=2π
分析可知，T与B、m无关．故A错误．
B、摆球在最低点时，根据左手定则判断可知，当小球向右运动时，小球所受的洛伦兹力方向向上，绳子的张力与洛伦兹力、重力的合力提供向心力，根据牛顿第二定律得：FO+qvB-mg=m
，则得FO=mg-qvB+m
；
在C点：绳子的张力 FC=mgcosα．比较上两式得知，摆球在最低点时，绳子的张力不一定比在C点时的张力大，故B错误．
C、摆球在最低点O的速度不为零，加速度不为零，为a=
．故C错误．
D、若不计空气阻力，绳子的张力与洛伦兹力不做功，摆球的机械能守恒．故D正确．
故选：D
|
B、摆球在最低点时，根据左手定则判断可知，当小球向右运动时，小球所受的洛伦兹力方向向上，绳子的张力与洛伦兹力、重力的合力提供向心力，根据牛顿第二定律得：FO+qvB-mg=m
| v2 |
| L |
| v2 |
| L |
在C点：绳子的张力 FC=mgcosα．比较上两式得知，摆球在最低点时，绳子的张力不一定比在C点时的张力大，故B错误．
C、摆球在最低点O的速度不为零，加速度不为零，为a=
| v2 |
| L |
D、若不计空气阻力，绳子的张力与洛伦兹力不做功，摆球的机械能守恒．故D正确．
故选：D
点评：洛伦兹力永远不做功，根据合力作为向心力来计算绳的拉力的大小，但要注意此时小球还受到洛伦兹力的作用，洛伦兹力的方向与速度有关．
练习册系列答案
相关题目
匝数为N、面积为S、总电阻为R的矩形闭合线圈，在磁感应强度为B的匀强磁场中按如图所示方向（俯视逆时针）以角速度ω绕轴OO′匀速转动．t=0时线圈平面与磁感线垂直，规定adcba的方向为电流的正方向．求：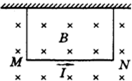
如图所示，一根通有电流I的直铜棒MN，用导线挂在磁感应强度为B的匀强磁场中，此时两根悬线处于紧张状态，当导线中通以水平向右的电流时，它受到的安培力方向为垂直导线