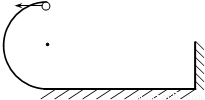
题目内容
半径为R的半圆形光滑轨道竖直放置，与粗糙水平轨道相接于最低点，水平轨道的最右端有一竖直挡板．今有一质量为m的小球从轨道最高点水平飞入轨道，飞入时对轨道的压力3mg．已知小球与水平轨道间的动摩擦因素为μ．（1）求小球第一次过半圆轨道最低点时对轨道压力的大小？
（2）小球第一次与挡板发生碰撞（碰撞过程中无机械能损失）后，恰能返回半圆轨道最高点，求水平轨道的长度．
【答案】分析：（1）、此题要找到几个状态，一是第一次经过最高点，二是第一次经过最低点，三是第二次经过最高点，对这三个状态进行分析．第一次经过最高点时，小球的重力和轨道最小球的支持力提供向心力，由向心力公式可求出此时的速度，由最高点到第一次经过最低点的过程中机械能守恒．应用能量关系求出速度v1，由向心力求出轨道对小球的支持力，再由牛顿第三定律可知小球对轨道的压力．
（2）、第二次回到最高点时，重力提供向心力，求出此时的速度v2，整个过程除重力做功外，还有摩擦力做功，由能量的转化和守恒可求出水平轨道的长度．
解答：解：
（1）、小球飞入轨道时的速度为v，第一次过最低点的速度为v1，受到的支持力为N1，则由圆周运动规律、机械能守恒定律得：
小球在最高点时：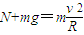
…①
小球在最低点时：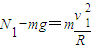
…②
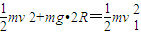…③
联立以上各式并代入数据得：N1=9mg
由牛顿第三定律得小球第一次过最低点时对轨道的压力：N1′=N1=9mg
（2）、由圆周运动规律、动能定理得：
恰能回到最高点时，有：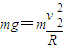
…④
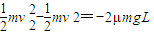…⑤
联立以上各式解得：
答：（1）求小球第一次过半圆轨道最低点时对轨道压力为9mg．
（2）水平轨道的长度为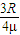
．
点评：小球在竖直平面内的圆形轨道内运动时，经过最高点的条件是速度
，当速度为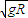
时，对轨道没有压力，此时只有重力提供向心力．
在解答第一问时，由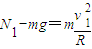
求得的N1是小球受到的支持力，问的是小球对管道的压力，此处一定要用牛顿第三定律．
（2）、第二次回到最高点时，重力提供向心力，求出此时的速度v2，整个过程除重力做功外，还有摩擦力做功，由能量的转化和守恒可求出水平轨道的长度．
解答：解：
（1）、小球飞入轨道时的速度为v，第一次过最低点的速度为v1，受到的支持力为N1，则由圆周运动规律、机械能守恒定律得：
小球在最高点时：
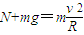…①小球在最低点时：
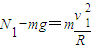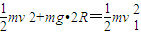…②…③联立以上各式并代入数据得：N1=9mg
由牛顿第三定律得小球第一次过最低点时对轨道的压力：N1′=N1=9mg
（2）、由圆周运动规律、动能定理得：
恰能回到最高点时，有：
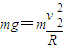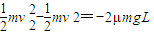…④…⑤联立以上各式解得：
答：（1）求小球第一次过半圆轨道最低点时对轨道压力为9mg．
（2）水平轨道的长度为
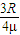．点评：小球在竖直平面内的圆形轨道内运动时，经过最高点的条件是速度
，当速度为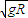时，对轨道没有压力，此时只有重力提供向心力．在解答第一问时，由
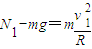求得的N1是小球受到的支持力，问的是小球对管道的压力，此处一定要用牛顿第三定律． 
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
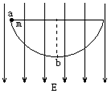如图所示，质量为m，带电量+q的小球置于半径为R的半圆形光滑轨道内，整个装置处于场强为E的竖直向下匀强电场中，小球从水平直径位置上的a点由静止释放，则小球经过最低点b时轨道对小球支持力的大小为
有一半径为R的半圆形光滑绝缘槽，置于水平向右的匀强电场中，若把一个带正电且电荷量为q、质量为m的小球放置在槽的B点时刚好静止，已知OB与竖直方向成37°角．若使小球从槽的边缘A点由静止滑下，求：（其中sin37°=0.6，cos37°=0.8）
如图所示，一半径为R的半圆形光滑轨道放在水平面上，A为轨道与水平面的切点，A左边的水平面是光滑的，半圆形光滑轨道固定．一个质量为m的小球以某一速度冲上轨道，小球落地点为C．当小球将要从轨道口飞出时，轨道的压力恰好为零．
如图所示，竖直光滑直轨道OA高度为2R，连接半径为R的半圆形光滑环形管道ABC（B为最低点），其后连接
如图所示，一半径为R的半圆形光滑轨道固定在竖直平面内．a、b是轨道的两端点且高度相同，O为圆心．小球A静止在轨道的最低点，小球B从轨道右端b点的正上方距b点高为2R处由静止自由落下，从b点沿圆弧切线进入轨道后，与小球A相碰．第一次碰撞后B球恰返回到b点，A球上升的最高点为c，Oc连线与竖直方向夹角为60°（两球均可视为质点）．求A、B两球的质量之比mA：mB．（结果可以用根式表示）