题目内容
 有一半径为R的半圆形光滑绝缘槽,置于水平向右的匀强电场中,若把一个带正电且电荷量为q、质量为m的小球放置在槽的B点时刚好静止,已知OB与竖直方向成37°角.若使小球从槽的边缘A点由静止滑下,求:(其中sin37°=0.6,cos37°=0.8)
有一半径为R的半圆形光滑绝缘槽,置于水平向右的匀强电场中,若把一个带正电且电荷量为q、质量为m的小球放置在槽的B点时刚好静止,已知OB与竖直方向成37°角.若使小球从槽的边缘A点由静止滑下,求:(其中sin37°=0.6,cos37°=0.8)(1)匀强电场的电场强度E大小.
(2)小球滑到最低点D时的速度vD.
(3)小球滑到最低点D时对槽的压力.
分析:(1)小球在B点受重力、电场力和支持力处于平衡,根据共点力平衡求出电场力的大小,从而得出匀强电场的场强大小.
(2)根据动能定理,求出小球滑到最低点D时的速度vD.
(3)在最低点时,由重力和轨道的支持力的合力提供小球的向心力,根据牛顿第二定律求解.
(2)根据动能定理,求出小球滑到最低点D时的速度vD.
(3)在最低点时,由重力和轨道的支持力的合力提供小球的向心力,根据牛顿第二定律求解.
解答: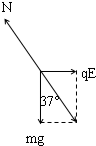 解:(1)小球位于B点时受力平衡,根据平衡条件qE=mgtan37°,解得E=
解:(1)小球位于B点时受力平衡,根据平衡条件qE=mgtan37°,解得E=
=
.
(2)小球由A滑到D的过程中,对小球运用动能定理:mgR-qER=
mvD2,得vD=
.
(3)小球运动到D点时由牛顿第二定律可知:FN-mg=m
所以FN=
mg
根据牛顿第三定律,小球对槽的压力为FN′=FN=
mg.
答:
(1)匀强电场的电场强度E大小是
.
(2)小球滑到最低点D时的速度vD是
.
(3)小球滑到最低点D时对槽的压力是
mg.
 解:(1)小球位于B点时受力平衡,根据平衡条件qE=mgtan37°,解得E=
解:(1)小球位于B点时受力平衡,根据平衡条件qE=mgtan37°,解得E=| mgtan37° |
| q |
| 3mg |
| 4q |
(2)小球由A滑到D的过程中,对小球运用动能定理:mgR-qER=
| 1 |
| 2 |
| ||
| 2 |
(3)小球运动到D点时由牛顿第二定律可知:FN-mg=m
| ||
| R |
所以FN=
| 3 |
| 2 |
根据牛顿第三定律,小球对槽的压力为FN′=FN=
| 3 |
| 2 |
答:
(1)匀强电场的电场强度E大小是
| 3mg |
| 4q |
(2)小球滑到最低点D时的速度vD是
| ||
| 2 |
(3)小球滑到最低点D时对槽的压力是
| 3 |
| 2 |
点评:解决本题的关键会根据共点力平衡,利用合成法求解力,以及会运用动能定理求小球的速度,掌握向心力的公式.

练习册系列答案
相关题目
 如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,电荷量为q带正电的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求:
如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,电荷量为q带正电的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求: 有一半径为R的半圆形光滑绝缘槽,置于水平向右的匀强电场中,把一个带电量为+q的质量为m的小8球放在槽的B点使OB与竖直方向夹角θ=60°时刚好静止.若使小球从槽的边缘A点由静止释放,求:
有一半径为R的半圆形光滑绝缘槽,置于水平向右的匀强电场中,把一个带电量为+q的质量为m的小8球放在槽的B点使OB与竖直方向夹角θ=60°时刚好静止.若使小球从槽的边缘A点由静止释放,求: 如图所示,有一半径为R的半圆形圆柱面MPQ,质量为2m的A球与质量为m的B球,用轻质绳连接后挂在圆柱面边缘.现将A球从边缘M点由静止释放,若不计一切摩擦,
如图所示,有一半径为R的半圆形圆柱面MPQ,质量为2m的A球与质量为m的B球,用轻质绳连接后挂在圆柱面边缘.现将A球从边缘M点由静止释放,若不计一切摩擦,