��Ŀ����
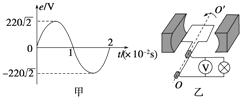
����Ŀ����ͼ��ʾ��ƽ�н�����P��Qˮƽ���ã���������Ϊd�������ڴ�ֱ��ƽ�н��������ǿ�糡�ʹ�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB1 �� �������Ʋ�ΪU����������Ϊm�������Ϊq�Ĵ���������ӣ���ijһ�ٶ��ش�ֱ�糡�ʹų��������������P��Q�䣬ǡ����ֱ��ͨ��ƽ�н����壮�����뿪���������ٷ���һ�ξ���������һ�߽�ΪԲ�ε���ǿ�ų�����δ��������Բ�������ڴų��ĴŸ�Ӧǿ�ȴ�СΪB2 �� ����ֱֽ�����⣬������Բ���������ٶȷ���ı�90��ʱ�뿪Բ��������������������������װ�ô�������У���
��1�������ٶȴ�С��
��2��������Բ��������������Բ���˶��Ĺ���뾶��
��3��Բ���������С�����
���𰸡�
��1��
�⣺�����ڽ�����P��Q��������ֱ���˶�
![]()
��ã�v= ![]()
�������ٶȴ�СΪ ![]()
��2��
�⣺��������Բ�δų���������Բ���˶��İ뾶ΪR�������������ṩ�������ã�
![]()
��ã�R= ![]()
��������Բ��������������Բ���˶��Ĺ���뾶 ![]()
��3��
�⣺������Բ�δų������˶��й켣��ͼ���ɼ��ι�ϵ֪��Բ�ĽǦ�=90�㣬�������֪��СԲ�δ�

���������� ![]() Բ�켣�ҳ�Ϊֱ����Բ����Բ���н�ų���Ϊr����
Բ�켣�ҳ�Ϊֱ����Բ����Բ���н�ų���Ϊr���� ![]()
����С���Ϊ��s=��r2= ![]()
��Բ���������С���Ϊ ![]()
����������1��������������ֱ��ͨ�����ϳ���������ֱ��������ƽ�������������ٶȵĴ�С����2�������������ṩ�����������������������Բ���˶��Ĺ���뾶����3��δ֪Բ���������Сֱ�����Թ켣Բ��Ӧ���ҳ�Ϊֱ�����ɴ˿������Բ���������С�����