题目内容
 如图所示,AB为
如图所示,AB为| 1 | 4 |
(1)物体在AB段克服阻力所做的功为多少?
(2)物体下滑到B点时对圆弧轨道的压力多大?
分析:(1)从A到C的运动的过程运用动能定理即可求解AB段克服阻力所做的功;
(2)从B到C的运动过程运用动能定理可解得到达B点时的速度,根据圆周运动向心力公式即可求得轨道对物体的支持力,根据牛顿第三定律可知,物体对轨道的压力等于轨道对物体的支持力;
(2)从B到C的运动过程运用动能定理可解得到达B点时的速度,根据圆周运动向心力公式即可求得轨道对物体的支持力,根据牛顿第三定律可知,物体对轨道的压力等于轨道对物体的支持力;
解答:解:(1)从A到C的运动的过程运用动能定理得:
mgR-Wf-μmgSBC=0
解得:Wf=6J
(2)从B到C的过程中,运用动能定理得:
-μmgSBC=0-
mvB2
解得:vB=2m/s
根据向心力公式得:N-mg=m
解得:N=15N
由牛顿第三定律可知,物体对轨道压力为15N
答:(1)物体在AB段克服阻力所做的功为6J;
(2)物体下滑到B点时对圆弧轨道的压力为15N.
mgR-Wf-μmgSBC=0
解得:Wf=6J
(2)从B到C的过程中,运用动能定理得:
-μmgSBC=0-
| 1 |
| 2 |
解得:vB=2m/s
根据向心力公式得:N-mg=m
| vB2 |
| R |
解得:N=15N
由牛顿第三定律可知,物体对轨道压力为15N
答:(1)物体在AB段克服阻力所做的功为6J;
(2)物体下滑到B点时对圆弧轨道的压力为15N.
点评:该题是圆周运动与匀变速直线运动相结合的典型题型,在不涉及到具体的运动过程和运动时间时用动能定理解题比较简洁、方便,要求同学跟根据题目的需要选择不同的运动过程运用动能动理解题,本题难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,AB为
如图所示,AB为 如图所示,AB为固定在竖直平面内的
如图所示,AB为固定在竖直平面内的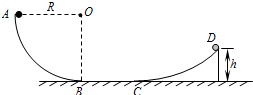 如图所示,AB为固定在竖直平面内的
如图所示,AB为固定在竖直平面内的 如图所示,AB为
如图所示,AB为