题目内容
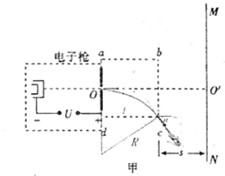
(2010?重庆模拟)如图甲所示,电子枪中的灯丝加热阴极而逸出电子,这些电子再经加速电场加速到很大速度后,从0点进入由磁偏转线圈产生的偏转磁场中,经过偏转匀强磁场后打到荧光屏MN上,使荧光屏发出荧光形成图象,不计逸出电子的初速度和重力.已知电子的质量为m、电荷量为e,加速电场的电压为u.偏转线圈产生的磁场分布在边长为L的正方形abcd区域内,磁场方向垂直纸面.磁场区域较小,左边界的中点与0点重合,ab边与00′平行,右边界bc与荧光屏之间的距离为s.
(1)求电子射出电场时的速度大小;
(2)为使电子恰能从磁场的bc边上边缘或下边缘射出,求偏转线圈磁场的磁感应强度B1;
(3)如果偏转线圈的磁感应强度随时间变化的规律如图乙所示,在每个周期内磁感应强度都是从-B0均匀变化到B0,且最大值B0与(2)问中的B1大小相等,荧光屏亮线的最大长度是多少?不计电子之间的相互作用.

(1)求电子射出电场时的速度大小;
(2)为使电子恰能从磁场的bc边上边缘或下边缘射出,求偏转线圈磁场的磁感应强度B1;
(3)如果偏转线圈的磁感应强度随时间变化的规律如图乙所示,在每个周期内磁感应强度都是从-B0均匀变化到B0,且最大值B0与(2)问中的B1大小相等,荧光屏亮线的最大长度是多少?不计电子之间的相互作用.

分析:(1)根据动能定理求出电子射出加速电场时的速度大小.
(2)根据几何关系求出临界状态下的半径的大小,结合洛伦兹力提供向心力求出磁感应强度的值.
(3)粒子在磁场中做匀速圆周运动,出磁场做匀速直线运动,通过最大的偏转角,结合几何关系求出荧光屏上亮线的最大长度.
(2)根据几何关系求出临界状态下的半径的大小,结合洛伦兹力提供向心力求出磁感应强度的值.
(3)粒子在磁场中做匀速圆周运动,出磁场做匀速直线运动,通过最大的偏转角,结合几何关系求出荧光屏上亮线的最大长度.
解答:解:(1)设电子射出电场的速度为v,则根据动能定理,对电子加速过程有
mv2=eU
解得:v=
(2)设偏转线圈磁场的磁感应强度为B1,电子在磁场中作匀速圆周运动,设此时圆周的半径为R
B1ev=
如图所示,
根据几何关系有:R2=L2+(R-
)2
解得B1=
(3)根据几何关系可知,tanα=
设电子打在荧光屏上离O′点的最大距离为d,
则d=
+s?tanα=
+
s
由于偏转磁场的方向随时间变化,根据对称性可知,荧光屏上的亮线最大长度为
D=L+
s;
答:(1)求电子射出电场时的速度
;
(2)为使电子恰能从磁场的bc边上边缘或下边缘射出,求偏转线圈磁场的磁感应强度B1为
;
(3)荧光屏亮线的最大长度是L+
s.
| 1 |
| 2 |
解得:v=
|
(2)设偏转线圈磁场的磁感应强度为B1,电子在磁场中作匀速圆周运动,设此时圆周的半径为R
B1ev=
| mv2 |
| R |
如图所示,

根据几何关系有:R2=L2+(R-
| L |
| 2 |
解得B1=
| 4 |
| 5L |
|
(3)根据几何关系可知,tanα=
| 4 |
| 3 |
设电子打在荧光屏上离O′点的最大距离为d,
则d=
| L |
| 2 |
| L |
| 2 |
| 4 |
| 3 |
由于偏转磁场的方向随时间变化,根据对称性可知,荧光屏上的亮线最大长度为
D=L+
| 8 |
| 3 |
答:(1)求电子射出电场时的速度
|
(2)为使电子恰能从磁场的bc边上边缘或下边缘射出,求偏转线圈磁场的磁感应强度B1为
| 4 |
| 5L |
|
(3)荧光屏亮线的最大长度是L+
| 8 |
| 3 |
点评:考查电子受电场力做功,应用动能定理;电子在磁场中,做匀速圆周运动,运用牛顿第二定律求出半径表达式;同时运用几何关系来确定半径与已知长度的关系.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 (2010?重庆模拟)在研究微型电动机的性能时,应用如图所示的实验电路.当调节滑动变阻器R并控制电动机停止转动时,电流表和电压表的示数分别为0.50A和2.0V.重新调节R并使电动机恢复正常运转,此时电流表和电压表的示数分别为2.0A和24.0V.则这台电动机正常运转时输出功率为( )
(2010?重庆模拟)在研究微型电动机的性能时,应用如图所示的实验电路.当调节滑动变阻器R并控制电动机停止转动时,电流表和电压表的示数分别为0.50A和2.0V.重新调节R并使电动机恢复正常运转,此时电流表和电压表的示数分别为2.0A和24.0V.则这台电动机正常运转时输出功率为( ) (2010?重庆模拟)如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星 O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为 R0,周期为T0.A 行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转.
(2010?重庆模拟)如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星 O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为 R0,周期为T0.A 行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转. (2010?重庆模拟)如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同,相对于地心,下列说法中正确的是( )
(2010?重庆模拟)如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同,相对于地心,下列说法中正确的是( )