题目内容
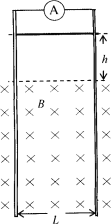
【题目】如图为一装放射源氡的盒子，静止的氡核经过一次α衰变成钋Po，新核Po的速率约为2×105m/s。衰变后的α粒子从小孔P进入正交的电磁场区域Ⅰ，且恰好可沿中心线匀速通过，磁感应强度B=0.1T。之后经过A孔进入电场加速区域Ⅱ，加速电压U=3×106V。从区域Ⅱ射出的α粒子随后又进入半径为r=
m的圆形匀强磁场区域Ⅲ，该区域磁感应强度B0=0.4T、方向垂直纸面向里。圆形磁场右边有一竖直荧光屏与之相切，荧光屏的中心点M和圆形磁场的圆心O、电磁场区域Ⅰ的中线在同一条直线上，α粒子的比荷为
=5×107C/kg。
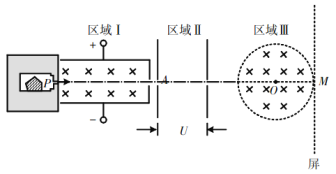
(1)请写出衰变方程，并求出α粒子的速率(保留一位有效数字)；
(2)求电磁场区域Ⅰ的电场强度大小；
(3)粒子在圆形磁场区域Ⅲ的运动时间多长？
(4)求出粒子打在荧光屏上的位置。
【答案】（1）
1×107 m/s
（2）1×106V/m
（3）
×10－7s
（4）打在荧光屏上的M点上方1 m处
【解析】
（1）根据质量数守恒和电荷数守恒写出方程，根据动量守恒求解速度；
（2）根据速度选择器的原理求解电场强度的大小；
（3）粒子在磁场中匀速圆周运动，并结合几何知识进行求解即可；
（1）根据质量数守恒和电荷数守恒，则衰变方程为： ①
设α粒子的速度为
，则衰变过程动量守恒：
②
联立①②可得：
③
（2）
粒子匀速通过电磁场区域Ⅰ：
④
联立③④可得：
⑤
（3）粒子在区域Ⅱ被电场加速：
所以得到：
⑥
粒子在区域Ⅲ中做匀速圆周运动： 
所以轨道半径为：
⑦
而且：
⑧
由图根据几何关系可知：粒子在磁场中偏转角
，所以粒子在磁场中的运动时间
⑨
联立⑧⑨可得：
；
（4）粒子的入射速度过圆心，由几何关系可知，出射速度方向也必然过圆心O，几何关系如图： 
，所以
，粒子打在荧光屏上的M点上方
处。
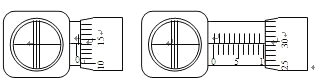
【题目】（1）在用双缝干涉测光的波长的实验中：⑴已知双缝到光屏之间的距离是600mm，双缝之间的距离是0.20mm，单缝到双缝之间的距离是100mm，某同学在用测量头测量时，先将测量头目镜中中看到的分划板中心刻线对准某条亮纹（记作第1条）的中心，这时手轮上的示数如左图所示。然后他转动测量头，使分划板中心刻线对准第7条亮纹的中心，这时手轮上的示数如右图所示。这两次示数依次为___ ________mm和___ mm。由此可以计算出这次实验中所测得的单色光的波长为____ ___nm。
（2）以下哪些操作能够增大光屏上相邻两条亮纹之间的距离( )
A．增大单缝和双缝之间的距离 | B．增大双缝和光屏之间的距离 |
C．将红色滤光片改为绿色滤光片 | D．增大双缝之间的距离 |
