题目内容
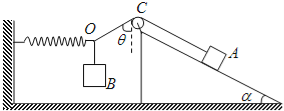
【题目】如图所示，两条足够长的光滑平行金属导轨相距为L，与水平面之间的夹角为θ，在整个区域都有垂直于导轨平面斜向上的磁感应强度大小为B的匀强磁场，在接近导轨底端附近导轨上放置一质量为m的导体棒MN，导体棒中点O通过一绝缘轻杆与固定在斜面底端的拉力传感器连接，轻杆与MN垂直，且与导轨平面平行，在导体棒MN上方有一始终与导轨垂直且接触良好的导体棒PQ，现给导体棒PQ一方向沿导轨平面向上的足够大的瞬时冲量I0（此时导体棒MN受到的安培力大于2mgsinθ），使导体棒PQ沿斜面向上运动，已知两导体棒的电阻均为R，导轨的电阻不计，重力加速度为g．
（1）求力传感器的最大示数；
（2）若已知导体棒PQ沿斜面向上运动的时间为t，求在导体棒PQ沿斜面向上运动的过程中，通过导体棒MN的电荷量；
（3）若已知导体棒PQ沿斜面向上运动的最大距离为x，求在导体棒PQ沿斜面向上运动的过程中，导体棒PQ产生的热量．
【答案】
（1）解：分析可知PQ棒刚开始运动时MN所受的安培力最大，又因为此时导体棒MN受到的安培力大于2mgsinθ，
对MN棒由平衡条件有：F=F安﹣mgsinθ ①
根据安培力公式可得：F安=BIL②
PQ获得向上初速度v0时，产生感应电动势为：E=BLv0 ③
根据动量定理可得：I0=mv0 ④
根据闭合电路欧姆定律有：I= 
⑤
联立①②③④⑤式可得：F= 
﹣mgsinθ
答：力传感器的最大示数为 ﹣mgsinθ；
（2）设沿斜面向上为正方向，根据动量定理有：﹣mgsinθt﹣BL∑I△t=0﹣mv0 ⑥
利用微积分，将过程分为无数个极短的小过程，则流过的电量：q=∑I△t ⑦
联立④⑥⑦式可得：q= 
答：在导体棒PQ沿斜面向上运动的过程中，通过导体棒MN的电荷量为 ；
（3）根据④可得v0= 
，
整个过程根据能量关系可得：Q= 
= 
，
所以导体棒PQ产生的热量QPQ= 
Q= 
．
答：若已知导体棒PQ沿斜面向上运动的最大距离为x，在导体棒PQ沿斜面向上运动的过程中，导体棒PQ产生的热量为 ．
【解析】（1）导体棒PQ向上做减速运动，产生的感应电动势和感应电流逐渐减小，MN所受的安培力方向沿导轨向上，大小不断减小，所以EF棒刚开始运动时MN所受的安培力最大，根据法拉第电磁感应定律、欧姆定律和安培力公式求出MN所受的安培力，由平衡条件求解传感器上的拉力；
（2）根据电荷量的经验公式
结合动量定理计算通过MN的电荷量；
（3）对两棒组成的系统，运用能量守恒定律列式求解导体棒MN产生的焦耳热;
对于电磁感应问题研究思路常常有两条：一条从力的角度，重点是分析安培力作用下导体棒的平衡问题，根据平衡条件列出方程；另一条是能量，分析涉及电磁感应现象中的能量转化问题，根据动能定理、功能关系等列方程求解。
【考点精析】关于本题考查的电磁感应与力学，需要了解用法拉第电磁感应定律和楞次定律求感应电动势的大小和方向；求回路中电流强度；分析研究导体受力情况（包含安培力，用左手定则确定其方向）；列动力学方程或平衡方程求解才能得出正确答案．
