Question

【题目】如图所示，一细U型管两端均开口，用两段水银柱封闭了一段空气柱在管的底部，初始状态气体温度为T1=280K,各段的长度分别为L1=20cm,L2＝15 cm，L3＝10 cm，h1＝4 cm，h2＝20 cm；现使气体温度缓慢升高，（大气压强为p0＝76 cmHg）求：

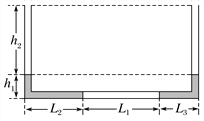
①若当气体温度升高到T2时，右侧水银柱开始全部进入竖直管，求此时左侧水银柱竖直部分有多高？并求出此时管底气柱的长L1′

②求第一问中的温度T2等于多少K?

③在T2的基础上继续升温至T3时,右侧水银柱变成与管口相平，求T3等于多少K?

Answer 1

【答案】①40cm ②630 K ③787.5 K

【解析】①因为左右两端管子均向上开口，所以气体压强p2＝p0＋h右=p0＋h左＝(76＋14)cmHg＝90 cmHg，所以左端液柱高度h左等于右端液柱高度h右，即h左=h左=14cm,

此时管底气柱的长度 L1′=L1+2L3=40cm

②设U型管的横截面积是S，以封闭气体为研究对象，

其初状态压强p1＝p0＋h1＝(76＋4) cmHg＝80 cmHg，

V1＝L1S＝20S,T1=280K

末状态是：p2＝p0＋h＝(76＋14) cmHg＝90 cmHg，V2＝L1′s=L1S＋2L3S＝20S＋2×10S＝40S, 由理想气体的状态方程得：

代入数据得：T2＝630K

③水银柱全部进入右管后，压强不再增大，管底气体做等压变化，所以左侧的水银柱不动，右侧水银柱与管口相平时，气体的体积：V3＝（L1′+h1+h2-L3-h1）s=(L1＋L3＋h2)s＝50S

由盖—吕萨克定律：

代入数据得：T3＝787.5 K.