题目内容
5.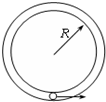 如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )
如图所示,可视为质点的、质量为m的小球,在半径为R的竖直放置的光滑圆形管道内做圆周运动,下列有关说法中正确的是( )| A. | 小球能够通过最高点时的最小速度为0 | |
| B. | 小球能够通过最高点时的最小速度为$\sqrt{gR}$ | |
| C. | 如果小球在最高点时的速度大小为2$\sqrt{gR}$,则此时小球对管道的外壁有作用力 | |
| D. | 如果小球在最高点时的速度大小为$\frac{\sqrt{gR}}{2}$,则此时小球对管道的外壁有作用力 |
分析 小球在光滑圆形管道中做圆周运动,最高点最小速度速度为零,当小球通过最高点的速度为2$\sqrt{gR}$和$\frac{\sqrt{gR}}{2}$,时,根据牛顿第二定律,结合径向的合力通过向心力求出轨道对球的作用力大小,根据正负得知方向.
解答 解:AB、小球在光滑圆形管道中做圆周运动,最高点最小速度速度为零,此时支持力等于重力,故A正确,B错误;
C、当最高点的速度为2$\sqrt{gR}$时,根据牛顿第二定律得:mg+N=m$\frac{{v}^{2}}{R}$解得:N=3mg,方向竖直向下,小球对管道的外壁有作用力,故C正确;
D、如果小球在最高点时的速度大小为$\frac{\sqrt{gR}}{2}$,根据牛顿第二定律得:mg+N=m$\frac{{v}^{2}}{R}$解得:N=-$\frac{3}{4}mg$,方向竖直向上,说明小球对管道的内壁有作用力,故D错误;
故选:AC
点评 解决本题的关键知道圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
14.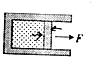 如图所示,一汽缸水平放置并固定,活塞左侧封闭有气体,已知活塞的横截面积为S,大气压强p0,活塞与汽缸壁间密合且无摩擦.现用一水平向右的力拉活塞,使封闭的气体体积恰好增加了2倍,保持温度不变,则拉力F的大小为( )
如图所示,一汽缸水平放置并固定,活塞左侧封闭有气体,已知活塞的横截面积为S,大气压强p0,活塞与汽缸壁间密合且无摩擦.现用一水平向右的力拉活塞,使封闭的气体体积恰好增加了2倍,保持温度不变,则拉力F的大小为( )
 如图所示,一汽缸水平放置并固定,活塞左侧封闭有气体,已知活塞的横截面积为S,大气压强p0,活塞与汽缸壁间密合且无摩擦.现用一水平向右的力拉活塞,使封闭的气体体积恰好增加了2倍,保持温度不变,则拉力F的大小为( )
如图所示,一汽缸水平放置并固定,活塞左侧封闭有气体,已知活塞的横截面积为S,大气压强p0,活塞与汽缸壁间密合且无摩擦.现用一水平向右的力拉活塞,使封闭的气体体积恰好增加了2倍,保持温度不变,则拉力F的大小为( )| A. | $\frac{{p}_{0}S}{3}$ | B. | $\frac{2{p}_{0}S}{3}$ | C. | $\frac{{p}_{0}S}{2}$ | D. | p0S |
10.在距地面高h处,甲球以初速度v0水平抛出,乙球同时以初速度v0沿45°的光滑斜面从高h处开始下滑,若它们同时到达地面,则初速度v0的大小是( )
| A. | $\frac{\sqrt{gh}}{2}$ | B. | $\sqrt{\frac{gh}{2}}$ | C. | $\sqrt{2gh}$ | D. | 2$\sqrt{gh}$ |
17.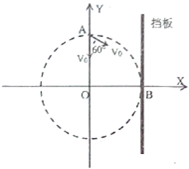 在直角坐标系XOY平面内有一磁场边界圆,半径为R,圆心在坐标原点O,圆内充满垂直该平面的匀强磁场,紧靠圆的右侧固定放置与Y轴平行的弹性挡板,如图所示.一个不计重力的带电粒子以速度v0从A点沿负Y方向进入圆内,刚好能垂直打在挡板B点上,若该粒子在A点速度v0向右偏离Y轴60°角进入圆内,粒子与档板相碰时间极短且无动能损失,则该粒子( )
在直角坐标系XOY平面内有一磁场边界圆,半径为R,圆心在坐标原点O,圆内充满垂直该平面的匀强磁场,紧靠圆的右侧固定放置与Y轴平行的弹性挡板,如图所示.一个不计重力的带电粒子以速度v0从A点沿负Y方向进入圆内,刚好能垂直打在挡板B点上,若该粒子在A点速度v0向右偏离Y轴60°角进入圆内,粒子与档板相碰时间极短且无动能损失,则该粒子( )
 在直角坐标系XOY平面内有一磁场边界圆,半径为R,圆心在坐标原点O,圆内充满垂直该平面的匀强磁场,紧靠圆的右侧固定放置与Y轴平行的弹性挡板,如图所示.一个不计重力的带电粒子以速度v0从A点沿负Y方向进入圆内,刚好能垂直打在挡板B点上,若该粒子在A点速度v0向右偏离Y轴60°角进入圆内,粒子与档板相碰时间极短且无动能损失,则该粒子( )
在直角坐标系XOY平面内有一磁场边界圆,半径为R,圆心在坐标原点O,圆内充满垂直该平面的匀强磁场,紧靠圆的右侧固定放置与Y轴平行的弹性挡板,如图所示.一个不计重力的带电粒子以速度v0从A点沿负Y方向进入圆内,刚好能垂直打在挡板B点上,若该粒子在A点速度v0向右偏离Y轴60°角进入圆内,粒子与档板相碰时间极短且无动能损失,则该粒子( )| A. | 在B点上方与挡板第二次相碰 | |
| B. | 经过$\frac{(π+1)R}{{v}_{0}}$时间第二次射出边界圆 | |
| C. | 第二次与挡板相碰时速度方向与挡板成60°角 | |
| D. | 经过$\frac{2πR}{{v}_{0}}$时间第二次与挡板相碰 |
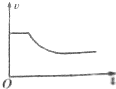
14.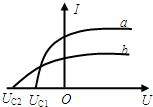 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则下列叙述正确的是( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则下列叙述正确的是( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则下列叙述正确的是( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则下列叙述正确的是( )| A. | 照射该光电管时a光使其逸出的光电子最大初动能大 | |
| B. | b光光子能量比a小 | |
| C. | 极限频率越大的金属材料逸出功越小 | |
| D. | 达到饱和光电流时,用a光照射光电管单位时间内逸出的光电子数多 |
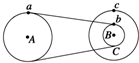 如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,则图中a、b、c各点的线速度之比va:vb:vc=1:1:2.
如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,则图中a、b、c各点的线速度之比va:vb:vc=1:1:2.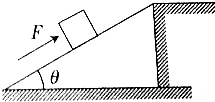 如图所示,斜面长l=5m,高h=3m,一工人借用这一斜面把质量m=25kg的木箱从斜面底端匀速推到斜面顶端(推力F的方向平行于斜面).已知木箱与斜面间的动摩擦因数μ=0.2,取g=10m/s2.求:
如图所示,斜面长l=5m,高h=3m,一工人借用这一斜面把质量m=25kg的木箱从斜面底端匀速推到斜面顶端(推力F的方向平行于斜面).已知木箱与斜面间的动摩擦因数μ=0.2,取g=10m/s2.求: