题目内容
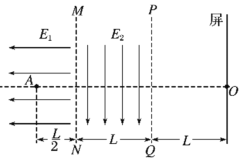
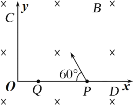
【题目】如图所示,在直角坐标系xOy平面内有一个磁感线垂直于xOy平面的匀强磁场,磁场的磁感应强度的大小为B,两个坐标轴上分别固定了很薄(厚度不计、长度足够)且垂直xOy平面的挡板OC、OD,在OD板上距离O点为L的P处固定有一个粒子源,从粒子源中射出的粒子均为电荷量+q、质量m的同种粒子,这些粒子的速率不同,进入磁场后的速度方向均在xOy平面内,且与OD板之间的夹角均为60°,经过一段时间的运动后均打在挡板上(打在挡板上的粒子均镶嵌在板内,不反弹也不穿过挡板),不计粒子的重力和粒子间的相互作用。求:
(1)打在Q点的粒子从P到Q的运动时间;
(2)垂直打在OC板上的粒子运动的速率。
【答案】(1) ![]() (2)
(2)![]()
【解析】
(1)如图所示,设打在Q点的粒子的轨迹圆弧Ⅰ的圆心为O1。
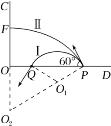
由几何关系可知:轨迹Ⅰ对应的圆心角∠PO1Q=120°,
由洛伦兹力充当向心力时的周期公式得
T=![]()
所求运动时间为
t1=![]()
联立解得
t=![]()
(2)设垂直打在OC板上的粒子的轨迹圆弧Ⅱ的圆心为O2、半径为R2。
由几何关系得
R2cos30°=L
由洛伦兹力充当向心力得
qv′B=m![]()
联立解得
v′=![]()

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】小明在测定一节干电池的电动势E和内阻r的实验中,管理员给他提供了如下器材:
A.待测的干电池(E≈1.5V,r≈1.0Ω) | E.滑动变阻器R2(0~20Ω,10A) |
B.电流表A1(0~3mA,Rg1=100Ω) | F.电阻箱R0(0~999Ω) |
C.电流表A2(0~0.6A,Rg2约为0.1Ω) | G.开关和导线若干 |
D.滑动变阻器R1(0~2kΩ,1A) |
(1)由于没有电压表管理员给小明设计了如图所示的甲、乙、丙、丁四个实验电路,并要求他用图像法处理实验数据,你认为应该选择图________作为实验电路,在你选择的电路中,为了操作方便且能更准确地进行测量,滑动变阻器应选________(填写器材前的字母代号)。

(2)小明选出合理的实验电路后,把与R0串联的电流表当作量程为0~3V的电压表使用,因此他应该将电阻箱R0的阻值调至________Ω。
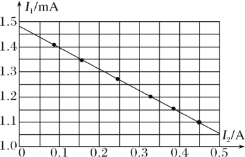
(3)小明选出合理的实验电路后,严格按照实验步骤和操作规范进行实验,测出了六组电流表A1的示数I1和电流表A2的示数I2,并绘出了如图所示的I1-I2图线,则被测干电池的电动势E=________V,内阻r=________Ω。(结果保留2位小数)