题目内容
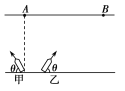
【题目】如图所示,质量为m=1.2kg的小球P(可以看成质点),用两根轻绳OP和O′P在P点拴结后再分别系于竖直墙上相距0.3m的O、O′两点上,绳OP长0.5 m,绳O′P长0.4 m,今在小球上施加一方向与水平成θ=37°角的拉力F,将小球缓慢拉起.当绳O′P和绳OP都处于绷紧状态时,拉力F 的取值范围是多少?(sin 37°=0.6,cos 37°=0.8,g =10m/s2)

【答案】![]()
【解析】
绳O′P刚拉直时,OP绳拉力为T1,此时O′P绳子拉力为零,小球受力如图所示,
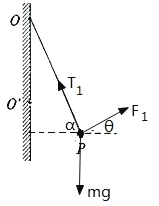
根据几何关系可得:sinα=OO′/OP
所以有:α=37
所以有:α+θ=90;
根据共点力的平衡条件可得:
F1cosθ=T1cosα
F1sinθ+T1sinα=mg
联立解得F1=10N;
绳OP刚松弛时,O′P绳拉力为T2,此时OP绳子拉力为零,小球受力如图所示,
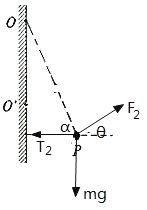
根据共点力的平衡条件可得:
F2=mg/sinθ=20N
由此可得,F的取值范围:10N<F<20N

练习册系列答案
相关题目