题目内容
【题目】如图所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为
的小球，其中
,两绳能承担的最大拉力相等且为F=40N,小球随转轴以定的角速度转动，AC和BC均拉直，此时
. ABC能绕竖直轴AB匀速转动，而C球在水平面内做匀速圆周运动(
)， 求： (结果保留三位有效数)
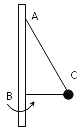
(1)当BC绳刚好拉直时，角速度多大?
(2)当小球的角速度增大时，通过计算判断AC和BC哪条绳先断?当先断的绳刚断时的角速度多大?
(3)一条绳被拉断后，为了让小球能够做圆周运动，则小球的最大线速度为多少?
【答案】（1）
（2）绳BC断，
（3）
【解析】
（1）当BC绳刚好拉直时，小球受AC绳的拉力
和重力
，对小球由：
水平方向：
竖直方向：
由以上方程解得：
（2）当BC绳刚好拉直后，AC绳和BC绳上的拉力分别为
和
，对小球由
竖直方向：
水平方向：
当小球的加速度增大时，绳AC的拉力不变，绳BC的拉力增大，所以绳BC先断。
由题意可知当
是，绳BC断，由以上方程化简可得此时的加速度：
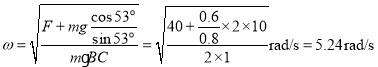
（3）当BC绳被拉断后，设AC绳与竖直方向的夹角为
，则：
由题意可知，的最大值为
由以上方程可知：
，即当是，对应线速度最大，则：
由几何知可知：
由以上方程解得：
练习册系列答案
相关题目
