题目内容
 (2011?辽宁二模)如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞.已知AB两点的高度差为h,重力加速度为g,不考虑空气阻力.求:
(2011?辽宁二模)如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞.已知AB两点的高度差为h,重力加速度为g,不考虑空气阻力.求:(1)小球在AB段运动过程中重力做功的平均功率P;
(2)小球落到C点时速度的大小.
分析:(1)根据匀变速直线运动的速度位移公式求出小球到达B点的速度,再根据平均速度公式求出这段位移内的平均速度,从而求出重力做功的平均功率.
(2)从B点反弹后做平抛运动,根据平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值,求出运动的时间,求出竖直分速度,根据平行四边形定则求出合速度,即C点的速度.
(2)从B点反弹后做平抛运动,根据平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值,求出运动的时间,求出竖直分速度,根据平行四边形定则求出合速度,即C点的速度.
解答:解:(1)小球下降过程中,做自由落体运动,落到斜面B点的速度为v,
满足:2gh=v2
解得:v=
所以小球在AB段重力的平均功率:P=mg
=
mg
(2)小球从B到C做平抛运动,设B到C的时间为t,
竖直方向:xBCsinθ=
gt2
水平方向:xBCcosθ=vt
解得:t=2
所以C点的速度为 vc=
=
.
满足:2gh=v2
解得:v=
| 2gh |
所以小球在AB段重力的平均功率:P=mg
. |
| v |
| ||
| 2 |
(2)小球从B到C做平抛运动,设B到C的时间为t,
竖直方向:xBCsinθ=
| 1 |
| 2 |
水平方向:xBCcosθ=vt
解得:t=2
|
所以C点的速度为 vc=
| v2+g2t2 |
| 10gh |
点评:解决本题的关键掌握求解平均功率的方法,可以根据P=mg
求解,也可以根据P=
求解.以及知道平抛运动竖直位移与水平位移的比值等于斜面倾角的正切值.
. |
| v |
| W |
| t |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?辽宁二模)“探究功能与物体速度变化的关系”的实验装置如图所示.
(2011?辽宁二模)“探究功能与物体速度变化的关系”的实验装置如图所示. (2011?辽宁二模)甲、乙两物体在同一地点,沿同一直线运动,其速度--时间图象如图所示,则( )
(2011?辽宁二模)甲、乙两物体在同一地点,沿同一直线运动,其速度--时间图象如图所示,则( )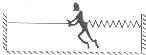 (2011?辽宁二模)运动员常利用如图所示的装置训练肌肉力量,弹簧右端与墙相连、左端系在运动员的腰上,左边墙上固定一根绳子.假定某运动员质量为50kg,他与地面间的动摩擦因数为μ=0.2,弹簧的劲度系数为k=1000N/m,运动员双手拉住绳子从弹簧原长位置向左缓慢前进(脚与地面间不打滑).当他向左运动的位移为3m时,运动员松开绳子被弹簧拉着向右滑行,若最大静摩擦力近似等于滑动摩擦力,g取10m/s2,则下列说法中不正确的是( )
(2011?辽宁二模)运动员常利用如图所示的装置训练肌肉力量,弹簧右端与墙相连、左端系在运动员的腰上,左边墙上固定一根绳子.假定某运动员质量为50kg,他与地面间的动摩擦因数为μ=0.2,弹簧的劲度系数为k=1000N/m,运动员双手拉住绳子从弹簧原长位置向左缓慢前进(脚与地面间不打滑).当他向左运动的位移为3m时,运动员松开绳子被弹簧拉着向右滑行,若最大静摩擦力近似等于滑动摩擦力,g取10m/s2,则下列说法中不正确的是( )