题目内容
4. 如图所示,两个质量均为m、带电量为-q的小球A和带电量为+q的小球B,固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上.另一端点用光滑铰链固定在O点.整个装置可以绕经过O点、且垂直于纸面的水平轴在竖直平面内自由转动,直角边的长度为L.空间有方向竖直向上.大小为E=$\frac{7mg}{q}$的匀强电场,将框架从图示位置(OB边水平、OA边竖直)由静止释放,重力加速度为g.求运动过中小球A的最大速度的大小.
如图所示,两个质量均为m、带电量为-q的小球A和带电量为+q的小球B,固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上.另一端点用光滑铰链固定在O点.整个装置可以绕经过O点、且垂直于纸面的水平轴在竖直平面内自由转动,直角边的长度为L.空间有方向竖直向上.大小为E=$\frac{7mg}{q}$的匀强电场,将框架从图示位置(OB边水平、OA边竖直)由静止释放,重力加速度为g.求运动过中小球A的最大速度的大小.
分析 设OB边转到与竖直方向成β角时,合力矩为零:qAE3Lcosβ-mgLcosβ+mgLsinβ-qBE3Lsinβ=0,解出β值,当框架转动90°+β时,小球速度最大.
能量守恒定律:qAE′(L+Lsinβ)+qBE′Lcosβ=mg(L+Lsinβ)+mgLcosβ+2×mv2代入数据计算最大速度
解答 解:设OB边转到与竖直方向成β角时,合力矩为零:
qAE3Lcosβ-mgLcosβ+mgLsinβ-qBE3Lsinβ=0
框架转动90°+β时,小球速度最大.
能量守恒定律:△E=△Ep+△Ek,
即qAE′(L+Lsinβ)+qBE′Lcosβ=mg(L+Lsinβ)+mgLcosβ+2×mv2
解出v=$\sqrt{2gL}$
答:运动过中小球A的最大速度的大小$\sqrt{2gL}$
点评 本题是关于竖直线对称的,但是不是图形的对称,而是需要力矩的对称,同样的一个力,需要在左边和右边时力臂是一样的

练习册系列答案
相关题目
15. 如图,在弯槽的顶端以初速度V释放一个小球,小球的动能为E,当到达B点时,球的动能是$\frac{3}{4}$E,速度是U;当以初速度2V释放小球,当达到B点时( )
如图,在弯槽的顶端以初速度V释放一个小球,小球的动能为E,当到达B点时,球的动能是$\frac{3}{4}$E,速度是U;当以初速度2V释放小球,当达到B点时( )
 如图,在弯槽的顶端以初速度V释放一个小球,小球的动能为E,当到达B点时,球的动能是$\frac{3}{4}$E,速度是U;当以初速度2V释放小球,当达到B点时( )
如图,在弯槽的顶端以初速度V释放一个小球,小球的动能为E,当到达B点时,球的动能是$\frac{3}{4}$E,速度是U;当以初速度2V释放小球,当达到B点时( )| A. | 球的动能等于3$\frac{3}{4}$E | B. | 球的速度小于$\sqrt{5}$U | ||
| C. | 球的速度等于$\sqrt{5}$U | D. | 球的动能小于3$\frac{3}{4}$E |
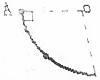
16.某同学利用如图(甲)所示的实验装置验证机械能守恒定律.实验所用电源为学生电源,输出电压为6V的交流电和直流电两种.图(乙)是他认为较理想的一条纸带,O点是打点计时器打出的第一个点(初速为零),A、B、C、D、E、F点是纸带上相邻的点.他们测出了各点与O点的距离h后做出了必要的计算,测量记录见下表
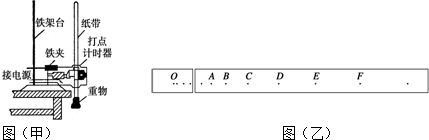
(1)距离h的记录中不符合有效数字读数的一组是A(填写计数点名称).
(2)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件
B.将打点计时器接到电源的“直流输出”上;
C.用天平测出重锤的质量
D.释放纸带,立即接通电源开关打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能
其中没有必要进行的或者操作不当的步骤是BCD(填选项对应的字母)
(3)打点计时器的频率为50Hz,则计时器打下C点时,重物的速度大小为1.56m/s;
(4)计数点C、D、E与O点之间的距离分别用hC、hD、hE表示,打点计时器的打点周期用T表示,若重物质量为m,重力加速度为g,则从O到D重物动能的增加量△Ek=$\frac{{m{{({h_E}-{h_C})}^2}}}{{8{T^2}}}$;O到D重物重力势能的减少量△EP=mghD(△Ek、△EP均用hC、hD、hE、T、m、g符号表示).

| 计数点 | A | B | C | D | E | F |
| h/cm | 6.9 | 9.47 | 12.40 | 15.71 | 19.41 | 23.49 |
(2)下面列举了该实验的几个操作步骤:
A.按照图示的装置安装器件
B.将打点计时器接到电源的“直流输出”上;
C.用天平测出重锤的质量
D.释放纸带,立即接通电源开关打出一条纸带;
E.测量纸带上某些点间的距离;
F.根据测量的结果计算重锤下落过程中减少的重力势能是否等于增加的动能
其中没有必要进行的或者操作不当的步骤是BCD(填选项对应的字母)
(3)打点计时器的频率为50Hz,则计时器打下C点时,重物的速度大小为1.56m/s;
(4)计数点C、D、E与O点之间的距离分别用hC、hD、hE表示,打点计时器的打点周期用T表示,若重物质量为m,重力加速度为g,则从O到D重物动能的增加量△Ek=$\frac{{m{{({h_E}-{h_C})}^2}}}{{8{T^2}}}$;O到D重物重力势能的减少量△EP=mghD(△Ek、△EP均用hC、hD、hE、T、m、g符号表示).
13. 如图所示,a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线,下列判断中正确的是( )
如图所示,a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线,下列判断中正确的是( )
 如图所示,a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线,下列判断中正确的是( )
如图所示,a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线,下列判断中正确的是( )| A. | a代表的电阻丝较粗 | |
| B. | b代表的电阻丝较粗 | |
| C. | a、b电阻并联之后的总电阻的伏安特性曲线应该落在 I 区域 | |
| D. | 图线表示的电阻丝的阻值与电压成正比 |
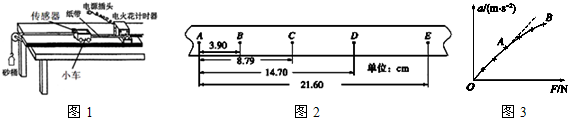
 一列简谐植被沿x轴方向传播,A、B是其中相距为0.5m的两点.在其时刻,A处质点正位于平衡位置向上运动,B处质点恰好运动到下方最大位移处.已知横波的传播速度为50m/s,波长大于0.5m.若该波沿x轴正方向传播,则波的频率为25Hz;若该波沿x轴负方向传播,则波的频率为75Hz.
一列简谐植被沿x轴方向传播,A、B是其中相距为0.5m的两点.在其时刻,A处质点正位于平衡位置向上运动,B处质点恰好运动到下方最大位移处.已知横波的传播速度为50m/s,波长大于0.5m.若该波沿x轴正方向传播,则波的频率为25Hz;若该波沿x轴负方向传播,则波的频率为75Hz.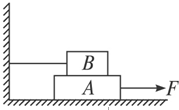 如图所示,物体A重20N,物体B重10N,物体A与物体B、物体A与地面的动摩擦因数相同,用细绳系住物体B,对物体A施加20N的水平向右的拉力时,能将物体A匀速拉出,求接触面间的动摩擦因数.
如图所示,物体A重20N,物体B重10N,物体A与物体B、物体A与地面的动摩擦因数相同,用细绳系住物体B,对物体A施加20N的水平向右的拉力时,能将物体A匀速拉出,求接触面间的动摩擦因数.