题目内容
10. 测速仪安装有超声波发射和接收装置,如图所示,B为测速仪,A为汽车,两者相距335m.某时刻B发出超声波,同时A由静止开始做匀加速直线运动.当B接收到反射回来的超声波信号时A、B相距355m,已知超声波传播速度为340m/s,则下列说法正确的是( )
测速仪安装有超声波发射和接收装置,如图所示,B为测速仪,A为汽车,两者相距335m.某时刻B发出超声波,同时A由静止开始做匀加速直线运动.当B接收到反射回来的超声波信号时A、B相距355m,已知超声波传播速度为340m/s,则下列说法正确的是( )| A. | 经2s,B接收到返回的超声波 | B. | 超声波追上A车时,A车前进了10m | ||
| C. | A车加速度的大小为10m/s2 | D. | A车加速度的大小为5m/s2 |
分析 在超声波来回运动的时间里,汽车运行的位移为20m.根据匀变速运动的位移时间公式可求出汽车在超声波单程运行时间里的位移,结合超声波的速度,即可知道超声波单程运行的时间,从而知道汽车运行的时间,根据x=$\frac{1}{2}a{t}^{2}$,求出汽车的加速度大小.
解答 解:设汽车的加速度为a,运动的时间为t,有$\frac{1}{2}a{t}^{2}=355-335m=20m$,超声波来回的时间为t,则单程的时间为$\frac{1}{2}t$,因为初速度为零的匀加速直线运动,在相等时间内的位移之比为1:3,在t时间内的位移为20m,则$\frac{1}{2}t$时间内的位移为x′=5m,知超声波追上汽车时,超声波的位移x=5+335m=340m,A车的位移为5m.故B错误.
根据$\frac{t}{2}=\frac{x}{{v}_{声}}=\frac{340}{340}s=1s$知,解得B接收到返回的超声波的时间t=2s,故A正确.
根据$\frac{1}{2}a{t}^{2}=20m$得,加速度a=10m/s2.故C正确,D错误.
故选:AC.
点评 解决本题的关键求出超声波单程运行的位移从而求出单程运行的时间,即可知道汽车匀加速运动的时间,然后根据匀变速运动的位移公式求出汽车的加速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.甲、乙两物体所受的重力之比为1:2,甲,乙两物体所在的位置高度之比为2:1,它们各自做自由落体运动,则( )
| A. | 落地时的速度之比是$\sqrt{2}$:1 | B. | 落地时的速度之比是1:1 | ||
| C. | 下落过程中的加速度之比是1:2 | D. | 落地的时间之比是1:2 |
18.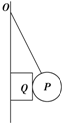 一根轻绳一端系小球P,另一端系于光滑墙壁上的O点,在墙壁和小球P之间夹有一矩形物块Q.如图所示,在小球P、物块Q均处于静止状态的情况下,下列有关说法正确的是( )
一根轻绳一端系小球P,另一端系于光滑墙壁上的O点,在墙壁和小球P之间夹有一矩形物块Q.如图所示,在小球P、物块Q均处于静止状态的情况下,下列有关说法正确的是( )
 一根轻绳一端系小球P,另一端系于光滑墙壁上的O点,在墙壁和小球P之间夹有一矩形物块Q.如图所示,在小球P、物块Q均处于静止状态的情况下,下列有关说法正确的是( )
一根轻绳一端系小球P,另一端系于光滑墙壁上的O点,在墙壁和小球P之间夹有一矩形物块Q.如图所示,在小球P、物块Q均处于静止状态的情况下,下列有关说法正确的是( )| A. | 物块Q一定受4个力 | |
| B. | 小球P可能受3个力 | |
| C. | 若轻绳变长,物块Q受到的静摩擦力将变小 | |
| D. | 若轻绳变长,绳子的拉力将变小 |
15.物体以速度v匀速通过直线上的A、B两点,所用时间为t,现在物体从A由静止出发,先匀加速直线运动(加速度大小为a1)到某一最大速度vm后立即做匀减速直线运动(加速度大小为a2)至B点速度恰好减为0,所用时间仍为t.则下列说法正确的是( )
| A. | a1一定大于a2 | |
| B. | a1、a2必须满足 $\frac{{a}_{1}•{a}_{2}}{{a}_{1}+{a}_{2}}$=$\frac{2v}{t}$ | |
| C. | vm只能为2v,与a1、a2的大小无关 | |
| D. | vm可为许多值,与a1、a2的大小有关 |
2.以v0=12m/s的速度匀速行驶的汽车,突然刹车,刹车过程中汽车以a=-6m/s2的加速度继续前进,则刹车后( )
| A. | 3s内的位移是9m | B. | 3s内的位移是12m | ||
| C. | 第2s内的位移是12m | D. | 3s未加速的大小是6m/s |

