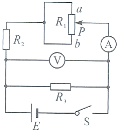
��Ŀ����
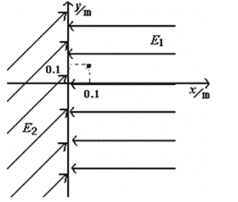
����Ŀ����ͼ��ʾ����y��Ϊ�߽磬�ұ���ˮƽ�����E1=1��104N/C��ǿ�糡���������ˮƽ�����45��б���ϵ�E2=![]() ��104N/C��ǿ�糡������һ������Ϊm=
��104N/C��ǿ�糡������һ������Ϊm=![]() kg��������q=1��10��6CС����������Ϊ��0.1m��0.1m������ֹ�ͷš�����������g=10m/s2�� ��[������Դ�����]
kg��������q=1��10��6CС����������Ϊ��0.1m��0.1m������ֹ�ͷš�����������g=10m/s2�� ��[������Դ�����]
��1�����ͷ�ʱ�ļ��ٶ�a
��2����һ�ξ���y��ʱ�����꼰ʱ��
��3���ڶ��ξ���y��ʱ������
���𰸡���1��10![]() m/s2��2����0��0��;
m/s2��2����0��0��;![]() s��3����0��-1.6m��
s��3����0��-1.6m��
��������
��1�� С�����ڵ糡E1���ܵ��糡��
![]()
�ܵ�������
mg=0.01N
����ָ��ԭ�㣬С�������ȼ���ֱ���˶�����һ�ξ���y��������ǣ�0��0��
���ٶ�Ϊ��
![]()
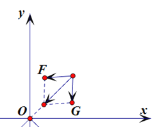
��2�� ���ͷŵ�ԭ��λ��S��
![]()
��![]() �ã�
�ã�
![]()
��һ�ξ���y��������ǣ�0��0��
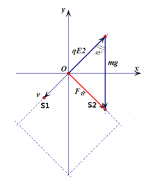
��3�� �˶���ԭ����ٶ�Ϊ��
![]()
�ڵ糡E2�У��糡��
![]()
F���������
![]()
ǡ�ú��ٶȴ�ֱ��
![]()
��������ƽ���˶�
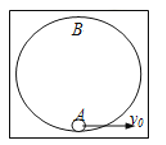
��ע�⣬��һ�������⣬�ռ���תһ�»������һ�㣬����ͼ��
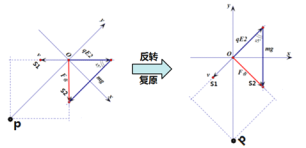
��ԭ���ٵ�y�ᣬ�س��ٶȷ������٣�
![]()
�ش�ֱ�ٶȷ���
![]()
���ң�
S1=S2
��ã�
![]()
�ڣ��λص�y���P�㣬
����Զ��ľ���
y=![]() =
=![]()
�ڶ��ξ���y��ʱ�����꣨0��-1.6m��

��ϰ��ϵ�д�
�����Ŀ