题目内容
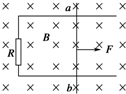如图所示，两光滑平行导轨水平放置在匀强磁场中，磁场垂直导轨所在平面，金属棒ab可沿导轨自由滑动，导轨一端跨接一个定值电阻R，导轨电阻不计．现将金属棒沿导轨由静止向右拉，若保持拉力F恒定，经过时间t1后速度为v，加速度为a1，最终以速度2v做匀速运动；若保持拉力的功率P恒定，棒由静止经时间t2后速度为v，加速度为a2，最终也以速度2v做匀速运动，则（ ）分析：分析清楚两种情况下的运动形式区别，然后根据牛顿第二定律和运动学规律求解，注意两种情况下导体棒最终匀速运动时所受拉力大小是相同的．
解答：解：C、D由于两种情况下，最终棒都以速度2v匀速运动，此时拉力与安培力大小相等，则有：
F=F安=BIL=BL?
=
①
当拉力恒定，速度为v，加速度为a1时，根据牛顿第二定律有：F-
=ma1 ②
由①②解得：a1=
．
若保持拉力的功率恒定，速度为2v时，拉力为F，则有：P=F?2v，
又F=F安=
所以P=
则当速度为v时，拉力大小为：F1=
=
；
根据牛顿第二定律，得：
F1-
=ma2，解得：a2=
，所以有a2=3a1，故CD错误；
A、B当拉力的功率恒定时，随着速度增大，拉力逐渐减小，最后匀速运动时拉力最小，且最小值和第一种情况下拉力相等，因此最后都达到速度2V时，t1＞t2，故A错误，B正确．
故选B
F=F安=BIL=BL?
| BL?2v |
| R |
| 2B2L2v |
| R |
当拉力恒定，速度为v，加速度为a1时，根据牛顿第二定律有：F-
| B2L2v |
| R |
由①②解得：a1=
| B2L2v |
| Rm |
若保持拉力的功率恒定，速度为2v时，拉力为F，则有：P=F?2v，
又F=F安=
| 2B2L2v |
| R |
所以P=
| 4B2L2v2 |
| R |
则当速度为v时，拉力大小为：F1=
| P |
| v |
| 4B2L2v |
| R |
根据牛顿第二定律，得：
F1-
| B2L2v |
| R |
| 3B2L2v |
| Rm |
A、B当拉力的功率恒定时，随着速度增大，拉力逐渐减小，最后匀速运动时拉力最小，且最小值和第一种情况下拉力相等，因此最后都达到速度2V时，t1＞t2，故A错误，B正确．
故选B
点评：本题可以和机车启动的两种方式进行类比解答，只不过机车启动时阻力不变，而该题中阻力为安培力，是不断变化的．
练习册系列答案
相关题目
（2006?静安区模拟）如图所示，两光滑平行导轨MN、PQ水平放置在匀强磁场中，磁场与导轨所在平面垂直，金属棒ab可沿导轨自由移动，导轨左端M、P接一定值电阻，金属棒和导轨电阻均不计，现将金属棒沿导轨由静止向右拉，若保持拉力F恒定，经时间t1后速度为v，加速度为a1，最终以速度2v做匀速运动；若保持拉力的功率不变，经过时间t2后，速度为v，加速度为a2，最终也以2v做匀速运动，求a1和a2的比值？
（2012?昆山市模拟）如图所示，两光滑平行导电导轨水平放置于磁感应强度为B的匀强磁场中，磁场与导轨所在平面垂直．已知金属棒ab能沿导轨自由移动，且导轨一端跨接一个定值电阻R，金属棒与导轨电阻均不计．现将金属棒沿导轨以初速度v0开始向右拉动，若保持拉力恒定不变，经过时间t1后金属棒速度变为v，加速度为a1，最终以速度2v做匀速运动．若再使金属棒仍以初速度v0开始，保持拉力的功率不变，经过时间t2后金属棒速度变为v，加速度为a2，最终以速度2v做匀速运动．则（ ）
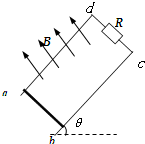如图所示，两光滑平行的金属导轨所在的平面与水平面成一角，导轨上端cd通过电阻R连接（不计电路中的其它电阻），匀强磁场垂直穿过导轨平面．若金属杆ab以沿平行于导轨平面大小为2| gh |
| A、上行过程中流过电阻R上的感应电流的方向是由c端流向d端 |
| B、上行时间小于下行时间 |
| C、上行过程中电阻R上产生的热量比下行时的大 |
| D、上行过程导体杆ab受到的磁场力的冲量的大小跟下行时的不相等 |