题目内容
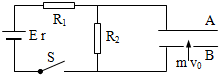 如图所示,两平行金属板A、B水平放置,板间距离d=40cm.电源电动势E=24V,内阻r=1Ω,电阻R1=15Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度V0=4m/s竖直向上射入板间,若小球带电量为q=1×10-2C,质量为m=2×10-2Kg,不考虑空气阻力,取g=10m/s2.那么,当R2的阻值为多少时,小球恰能到达A板?
如图所示,两平行金属板A、B水平放置,板间距离d=40cm.电源电动势E=24V,内阻r=1Ω,电阻R1=15Ω.闭合开关S,待电路稳定后,将一带正电的小球从B板小孔以初速度V0=4m/s竖直向上射入板间,若小球带电量为q=1×10-2C,质量为m=2×10-2Kg,不考虑空气阻力,取g=10m/s2.那么,当R2的阻值为多少时,小球恰能到达A板?分析:根据匀变速直线运动的速度位移关系v2-v02=2ad,然后根据匀变速直线运动的速度位移关根据牛顿第二定律mg+Eq=ma,计算AB间的电场强度,根据匀强电场的电场强度与电势差的关系UAB=Ed,计算AB间的电势差.最后根据欧姆定律求解滑动变阻器的电阻值.
解答:解:小球受到重力和电场力两个恒力,故做匀减速直线运动,根据速度与位移的关系
0-v02=2ad
得:a=-20m/s2
对小球受力分析,受到竖直向下的重力、竖直向下的电场力,根据牛顿第二定律mg+Eq=ma
所以AB间的电场强度为E=20N/c
AB间的电势差为:UAB=Ed=20×0.4V=8V
设通过R2电流为I,滑动变阻器两端电压等于AB间的电势差,由欧姆定律得
I=
=1A
滑动变阻器接入电路的电阻
R2=
=8Ω
答:当R2的阻值为8Ω时,小球恰能到达A板.
0-v02=2ad
得:a=-20m/s2
对小球受力分析,受到竖直向下的重力、竖直向下的电场力,根据牛顿第二定律mg+Eq=ma
所以AB间的电场强度为E=20N/c
AB间的电势差为:UAB=Ed=20×0.4V=8V
设通过R2电流为I,滑动变阻器两端电压等于AB间的电势差,由欧姆定律得
I=
| E-UAB |
| R1+r |
滑动变阻器接入电路的电阻
R2=
| UAB |
| R2 |
答:当R2的阻值为8Ω时,小球恰能到达A板.
点评:本题属于偏难点的力学综合题,求AB间电势差时也可根据动能定理求解.

练习册系列答案
相关题目
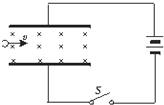 如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )
如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )| A、把两板间距离减小一半,同时把粒子速率增加一倍 | B、把两板的距离增大一倍,同时把板间的磁感应强度增大一倍 | C、把开关S断开,两板的距离增大一倍,同时把板间的磁感应强度减为一半 | D、把开关S断开,两板的距离减小一半,同时把粒子速率减小一半 |
 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )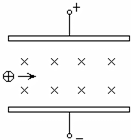 如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( )
如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( ) 如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( )
如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( ) 如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=
如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=