题目内容
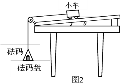
【题目】如图1所示,一小车放于平直木板上(木板一端固定一个定滑轮),木板被垫高一定角度θ,该角度下,小车恰能做匀速直线运动(假设小车所受摩擦力与小车对木板的正压力成正比,比例系数为μ),小车总质量为M。

(1)请推导θ与μ应满足的定量关系;并分析说明若增大小车质量,仍使小车做匀速直线运动,角度θ是否需要重新调整。
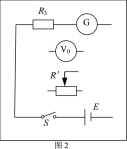
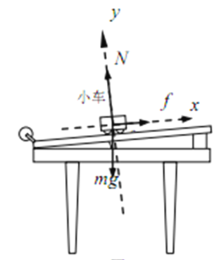
(2)如图2所示,将小车上栓一根质量不计,且不可伸长的细绳,细绳通过滑轮(滑轮与细绳之间摩擦不计)下挂一个砝码盘(内放砝码),在木板上某位置静止释放小车后,小车做匀加速直线运动。已知砝码盘及砝码的总质量为m,求:
①a.如果m=M,小车所受细绳拉力与砝码盘及砝码总重力的比值;
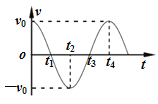
b.用F表示小车所受细绳的拉力,如果要求![]() ,此时
,此时![]() 应该满足的条件;
应该满足的条件;
②小车沿木板运动距离为x的过程中,其机械能的变化量ΔE。
【答案】(1)μ=tanθ;增大小车的质量,角度θ无须改变。(2)①a.![]() b.
b. ![]() ②
②![]()
【解析】
(1)受力分析如图:重力的下滑分力为![]() ,小车受到的摩擦力为:
,小车受到的摩擦力为:![]()
小车匀速运动,由平衡条件可得:![]()
解得![]()
论证:当小车的质量由M变成M+m时,若使小车匀速运动,仍有![]() 成立,仍然满足:
成立,仍然满足:![]() ,即若增大小车的质量,角度θ无须改变。
,即若增大小车的质量,角度θ无须改变。
(2)根据牛顿第二定律:①a.对小车由牛顿第二定律可得![]() ;对砝码和砝码盘由牛顿第二定律可得:
;对砝码和砝码盘由牛顿第二定律可得:![]() 由于
由于![]() 则
则![]() 的到:
的到:![]()
b.利用a中得到的结论:![]() 解得
解得![]() 可得
可得![]()
②小车沿木板运动距离为x的过程中,机械能的变化量等于小车所受的拉力和摩擦力做功的总和,则:![]()

练习册系列答案
相关题目