��Ŀ����
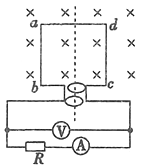
����Ŀ����ͼ��ʾ����ƽ�й⻬��������̶��ھ�Եб���ϣ�������ΪL������ϵ��Ϊk�����ʵ����϶˹̶����¶���ˮƽֱ�����ab�����������뵼��ƽ��ƽ�в���ab��ֱ��ֱ�������ֱ������������ϣ��ռ���ڴ�ֱ����ƽ��б���ϵ���ǿ�ų����պϿ���K������еĵ���ΪI�������ƽ��ʱ�������쳤��Ϊx1����תͼ�е�Դ����ʹ���е�����������е�����ΪI�������ƽ��ʱ�����쳤��Ϊx2.���Ի�·�е��������Ĵų�����Ÿ�Ӧǿ��B�Ĵ�СΪ�� ��

A. ![]() (x2��x1) B.
(x2��x1) B. ![]() (x2��x1)
(x2��x1)
C. ![]() (x2��x1) D.
(x2��x1) D. ![]() (x1��x2)
(x1��x2)
���𰸡�B
�������������쳤��Ϊx1ʱ����������ܰ�������б�����ϣ�����ƽ��������б�淽���У�mgsin��=kx1+BIL�����������������ܰ�������б�����£�����ƽ��������б�淽��mgsin��+BIL=kx2��������ʽ�ã�B=![]() ��x2-x1����ѡB��
��x2-x1����ѡB��

��ϰ��ϵ�д�
�����Ŀ