题目内容
3.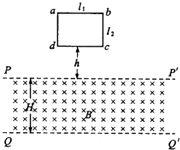 如图所示,矩形平面导线框abcd位于竖直平面内,水平边ab长l1,竖直边bc长l2,线框质量为m,电阻为R.线框下方有一磁感应强度为B、方向与线框平面垂直的匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行,两边界间的距离为H,H>l2.让线框从dc边距边界PP′的距离为h处自由下落,已知在dc边进人磁场后、ab边到达边界PP′前的某一时刻,线框的速度已达到这一阶段的最大值,重力加速度为g,则( )
如图所示,矩形平面导线框abcd位于竖直平面内,水平边ab长l1,竖直边bc长l2,线框质量为m,电阻为R.线框下方有一磁感应强度为B、方向与线框平面垂直的匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行,两边界间的距离为H,H>l2.让线框从dc边距边界PP′的距离为h处自由下落,已知在dc边进人磁场后、ab边到达边界PP′前的某一时刻,线框的速度已达到这一阶段的最大值,重力加速度为g,则( )| A. | 当dc边刚进磁场时,线框速度为$\sqrt{2gh}$ | |
| B. | 当ab边刚到达边界PP′时,线框速度为$\frac{mgR}{{B}^{2}{{l}_{2}}^{2}}$ | |
| C. | 当dc边刚到达边界QQ′时,线框速度为$\sqrt{(\frac{mgR}{{B}^{2}{{l}_{1}}^{2}})^{2}+2g(H-{l}_{2})}$ | |
| D. | 从线框开始下落到dc边刚到达边界的QQ′过程中,线框产生的焦耳热为mg(h+l2)-$\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{{l}_{2}}^{4}}$ |
分析 线框匀速进入磁场,重力与安培力平衡.安培力与速度成正比,根据安培力经验公式 F=$\frac{{B}^{2}{L}^{2}V}{R}$,由安培力可求出速度.根据能量守恒求解焦耳热.
由动能定理和功的计算公式,求出重力做的功W
解答 解:A、根据动能定理得:mgh=$\frac{1}{2}m{v}^{2}$,故当dc边刚进磁场时,线框速度为$\sqrt{2gh}$.故A正确.
B、当dc边受的安培力F=$\frac{{B}^{2}{L}^{2}V}{R}$=mg时,线框速度达到最大,大小 v=$\frac{mgR}{{B}^{2}{L}^{2}}$,其中L=L1,故B错误.
C、从ab边进入磁场到dc边到达QQ′边时,应用动能定理得:mg(H-L2)=$\frac{1}{2}m(V{′}^{2}-{V}^{2})$,解得:V′=$\sqrt{(\frac{mgR}{{B}^{2}{{l}_{1}}^{2}})^{2}+2g(H-{l}_{2})}$,故C正确
D、从线框开始下落到dc边刚到达边界的QQ′过程中,由动能定理:mg(h+H)=$\frac{1}{2}mV{′}^{2}+Q$,线框产生的焦耳热Q=$mg(h+{L}_{2})-\frac{{m}^{3}{g}^{2}{R}^{2}}{2{B}^{4}{L}_{1}^{4}}$,D错误.
故选:AC
点评 本题是电磁感应中的力学问题,求解安培力和分析能量如何转化是两个关键,考查电磁感应、动能定理、平衡条件等知识综合应用和分析能力

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
3.某种气体的温度是0℃,可以说( )
| A. | 气体中分子的温度是0℃ | |
| B. | 气体中分子运动的速度快的温度一定高于0℃,运动慢的温度一定低于0℃,所以气体平均温度是0℃ | |
| C. | 气体温度升高时,速率小的分子数目减少,速率大的分子数目增加 | |
| D. | 该气体没有内能 |
4.日常生活中,我们应该注意安全用电,下列做法中不符合安全规范的是( )
| A. | 洗衣机使用三孔插座 | B. | 用粗铜线代替保险丝 | ||
| C. | 家庭电路中接入漏电保护开关 | D. | 厨房中的电器应尽量远离水池 |
11.英国物理学家法拉第提出了“电场”和“磁场”的概念,并引入电场线和磁感线来描述电场和磁场,为经典电磁学理论学理论的建立奠定了基础.下列相关说法正确的是( )
| A. | 电荷和电荷、通电导体和通电导体之间的相互作用都是通过电场发生的 | |
| B. | 磁极和磁极、磁体和通电导体之间的相互作用都是通过磁场发生的 | |
| C. | 电场线和电场线不可能相交,磁感线和磁感线可能相交 | |
| D. | 通过实验可以发现电场线和磁感线是客观存在的 |
18.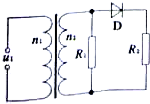 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=22:5,原线圈接u1=220$\sqrt{2}$sin100πt(V)的交流电,电阻R1=R2=25Ω,D为理想二极管,则下列说法不正确的是( )| A. | 电阻R1两端的电压为50V | B. | 二极管的反向耐压值应大于50$\sqrt{2}$V | ||
| C. | 原线圈的输入功率为200W | D. | 通过R2的电流为$\sqrt{2}$A |
8.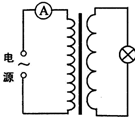 如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )
如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )
 如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )
如图所示,理想变压器原、副线圈匝数之比为10:1,原线圈接在频率为50Hz的正弦交流电源上,串接的电流表为理想电流表,副线圈接入“220V 60W”灯泡一只,此时灯泡正常发光.由此可知( )| A. | 电流表的示数约为0.27A | B. | 原线圈两端电压最大值为2200$\sqrt{2}$V | ||
| C. | 电源的输出功率为6W | D. | 副线圈中交变电流的频率为5Hz |
13.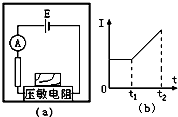 压敏电阻的阻值随着所受压力的增大而减小,在升降机中将重物放在压敏电阻上,压敏电阻接在如图(a)所示的电路中,电流表的示数变化情况如图(b)所示.某同学根据电流表的示数变化情况推断升降机的运动情况.下列推断正确的是( )
压敏电阻的阻值随着所受压力的增大而减小,在升降机中将重物放在压敏电阻上,压敏电阻接在如图(a)所示的电路中,电流表的示数变化情况如图(b)所示.某同学根据电流表的示数变化情况推断升降机的运动情况.下列推断正确的是( )
 压敏电阻的阻值随着所受压力的增大而减小,在升降机中将重物放在压敏电阻上,压敏电阻接在如图(a)所示的电路中,电流表的示数变化情况如图(b)所示.某同学根据电流表的示数变化情况推断升降机的运动情况.下列推断正确的是( )
压敏电阻的阻值随着所受压力的增大而减小,在升降机中将重物放在压敏电阻上,压敏电阻接在如图(a)所示的电路中,电流表的示数变化情况如图(b)所示.某同学根据电流表的示数变化情况推断升降机的运动情况.下列推断正确的是( )| A. | 0-t1时间内,升降机一定匀速运动 | |
| B. | 0-t1时间内,升降机可能减速上升 | |
| C. | t1-t2时间内,升降机可能匀速上升 | |
| D. | t1-t2时间内,升降机可能匀加速上升 |
 如图,MNPQ是一块截面为正方形的玻璃砖,其边长MN=60cm,一束激光沿AB射到玻璃砖的MQ面上(入射点为B),进入玻璃砖后在QP面上的F点(图中未画出)发生全反射,恰沿DC方向射出.其中B为MQ的中点,∠ABM=30°,PD=15cm,∠CDN=30°求
如图,MNPQ是一块截面为正方形的玻璃砖,其边长MN=60cm,一束激光沿AB射到玻璃砖的MQ面上(入射点为B),进入玻璃砖后在QP面上的F点(图中未画出)发生全反射,恰沿DC方向射出.其中B为MQ的中点,∠ABM=30°,PD=15cm,∠CDN=30°求