题目内容
【题目】地面上有一个半径为 R 的圆形跑道，高为 h 的平台边缘上的 P 点在地面 上 P′点的正上方， P′与跑道圆心 O 的距离为 L（L>R），如图所示。跑道上停有一辆小车， 现从 P 点水平抛出小沙袋，使其落入小车中（沙袋所受空气阻力不计）。问：
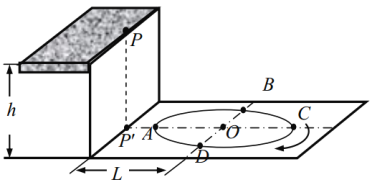
（1）当小车分别位于 A 点和 B 点时（∠AOB＝90° ），沙袋被抛出时的初速度各多大？
（2）若小车在跑道上运动，则沙袋被抛出时的初速度在什么范围内 ？
（3）若小车沿跑道顺时针运动（如图中箭头所示），当小车恰好经过 A 点时，将沙袋 抛出，为使沙袋能在 B 处落入小车中，小车的速率v 应满足什么条件？
【答案】（1）vA=（L-R）
；
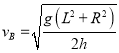（2）（L-R）≤v0≤（L+R）
（3）v=
（4n+1）πR（n=0，1，2，3…）．
【解析】
试题分析：（1）沙袋从P点被抛出后做平抛运动，设它的落地时间为t，则h=
gt2
解得
（1）
当小车位于A点时，有xA=vAt=L-R（2）
解（1）（2）得vA=（L-R）
当小车位于B点时，有
（3）
解（1）（3）得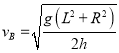
（2）若小车在跑道上运动，要使沙袋落入小车，最小的抛出速度为
v0min=vA=（L-R）（4）
若当小车经过C点时沙袋刚好落入，抛出时的初速度最大，有xc=v0maxt=L+R （5）
解（1）（5）得 v0max=（L+R）
所以沙袋被抛出时的初速度范围为（L-R）≤v0≤（L+R）
（3）要使沙袋能在B处落入小车中，小车运动的时间应与沙袋下落时间相同
tAB=（n+
）
（n=0，1，2，3…）（6）
所以tAB=t=
解得v=（4n+1）πR（n=0，1，2，3…）．
练习册系列答案
相关题目
