题目内容
1. 1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图11所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q 初速度可不计,在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.
1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图11所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q 初速度可不计,在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用.(1)求粒子第1次经过两D形盒间狭缝后的轨道半径?
(2)求粒子从开始被加速到由出口处射出,在磁场中的运动总时间t?
分析 (1)带电粒子在磁场中做匀速圆周运动,根据动能定理和洛伦兹力提供向心力求出轨道半径与加速电压的关系,从而求出轨道半径之比.
(2)通过D形盒的半径求出粒子的最大速度,结合动能定理求出加速的次数,一个周期内加速两次,从而得知在磁场中运动的周期次数,确定出粒子从静止开始加速到出口处所需的时间.
解答 解:(1)设粒子第1次经过狭缝后的半径为r1,速度为v1,由动能定理有:qu=$\frac{1}{2}$mv12
洛伦兹力提供向心力,则有:qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
联立解得:r1=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$
(2)设粒子到出口处被加速了n圈解得,由动能定理有:2nqU=$\frac{1}{2}$mv2
由牛顿第二定律有:qvB=m$\frac{{v}^{2}}{R}$
由周期公式有:T=$\frac{2πm}{qB}$
且t=nT
解上四个方程得:t=$\frac{πB{R}^{2}}{2U}$
答:(1)粒子第1次经过两D形盒间狭缝后的轨道半径$\frac{1}{B}\sqrt{\frac{2mU}{q}}$;
(2)粒子从开始被加速到由出口处射出,在磁场中的运动总时间t
点评 解决本题的关键掌握回旋加速器的原理,运用电场加速和磁场偏转,知道粒子在磁场中运动的周期与加速电场的变化周期相等.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
11.关于自由落体运动,下列说法正确的是( )
| A. | 物体从静止开始下落的运动叫自由落体运动 | |
| B. | 物体在只有重力作用下的运动叫做自由落体运动 | |
| C. | 在有空气的空间里,如果空气阻力与重力相比可以忽略不计,物体从静止开始下落的运动可以看做自由落体运动 | |
| D. | 在地球上不同的地方,自由落体加速度的大小是不同的,它们相差很大 |
9.图中的实线为点电荷的电场线,M、N 两点在以点电荷为圆心的同一圆上,下列说法正确的是( )

| A. | M 处的电场强度比 N 处的大 | |
| B. | M 处的电场强度比 N 处的小 | |
| C. | M、N 处的电场强度大小相等,方向相同 | |
| D. | M、N 处的电场强度大小相等,方向不同 |
16.下列关于分子斥力的说法正确的是( )
| A. | 一块玻璃破裂成两块不能直接拼接,是由于分子间斥力造成 | |
| B. | 给自行车打气时气筒压下后反弹,是由分子斥力造成 | |
| C. | 固体压缩后撤力恢复原状,是由于分子间存在斥力造成 | |
| D. | 将香水瓶打开满室飘香,是由于香水分子间斥力造成 |
6.下列说法正确的是( )
| A. | 只要自由电荷运动必定会形成电流 | B. | 有自由电荷就能形成电流 | ||
| C. | 形成电流必须要有电势差 | D. | 有电源就有电流 |
7.继哥白尼提出”太阳中心说”,开普勒提出行星运动三定律后,牛顿站在巨人的肩膀上,创立了经典力学,揭示了包括行星在内的宏观物体的运动规律.爱因斯坦既批判了牛顿力学的不足,又进一步发展了牛顿的经典力学,创立了相对论.这说明( )
| A. | 世界无限大,人不可能认识世界 | |
| B. | 人的意识具有能动性,能够随意地对客观世界说三道四 | |
| C. | 人对世界的每一个正确认识都有局限性,需要发展和深化 | |
| D. | 每一个认识都可能被后人推翻,人都不可能获得正确的认识 |
8.质量为2kg的质点,在两个力F1=2N、F2=8N的共同作用下,获得的加速度大小不可能的是( )
| A. | 5 m/s2 | B. | 3 m/s2 | C. | 1 m/s2 | D. | 4 m/s2 |
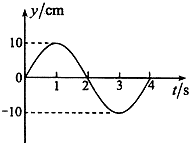 波源A点做简谐运动的振动图象如图所示,波源振动9s后,波传播方向上的B点第一次到达波谷,已知A、B两点的平衡位置相距12m,求这列波的波速大小.
波源A点做简谐运动的振动图象如图所示,波源振动9s后,波传播方向上的B点第一次到达波谷,已知A、B两点的平衡位置相距12m,求这列波的波速大小.