题目内容
（2011?泰兴市模拟）如图所示，一修路工在长为S=100m的隧道中，突然发现一列火车出现在离右隧道口200m处，修路工所处的位置恰好处在无论向左还是向右跑均能脱离危险的位置，问这个位置离隧道右出口的距离是多少？他奔跑的最小速度至少应是火车速度的多少倍？分析：工人向右运动时当运动到隧道右端时火车刚好也到达右端；工人向左运动到达隧道左端时，火车也刚好到达隧道左端，分别列出方程求解即可．
解答：解：设火车速度为v，人的速度为nv，人距离隧道右端的距离为x，距离左端的长度为（100-x），
当人向右运动时设到隧道右端需要时间为t1：
人向右匀速运动位移为x时，有：（nv）t1=x ①
此过程，火车的运动有：vt1=200 ②
①②两式取比值整理得：200n=x ③
当人向左运动时设到隧道左端需要时间为t2：
人的运动：nvt2=100-x ④
火车的运动：vt2=200+100 ⑤
④⑤两式取比值整理得：300n=100-x ⑥
由③⑥两式解得：n=
x=40m
答：这个位置离隧道右出口的距离是40m，他奔跑的最小速度至少应是火车速度的n=
倍．
当人向右运动时设到隧道右端需要时间为t1：
人向右匀速运动位移为x时，有：（nv）t1=x ①
此过程，火车的运动有：vt1=200 ②
①②两式取比值整理得：200n=x ③
当人向左运动时设到隧道左端需要时间为t2：
人的运动：nvt2=100-x ④
火车的运动：vt2=200+100 ⑤
④⑤两式取比值整理得：300n=100-x ⑥
由③⑥两式解得：n=
| 1 |
| 5 |
x=40m
答：这个位置离隧道右出口的距离是40m，他奔跑的最小速度至少应是火车速度的n=
| 1 |
| 5 |
点评：解决追及问题是注意它们在运动时间上具有等时性，然后根据位移找准相遇时的关系式．
练习册系列答案
相关题目
（2011?泰兴市模拟）如图斜面ABC，AB段是光滑的，BC段是有摩擦．某物体从A点由静止开始下滑，当滑至C点时恰好停止，则下列说法正确的是（ ）
（2011?泰兴市模拟）如图所示，物体A的质量m=3kg，用两根轻绳B、C连接于竖直墙上，要使两绳都能绷直，即物体A在如图所示位置保持平衡，现施加一个力F作用于物体，力F的方向如图所示，若夹角θ=60°，求力F的大小应满足的条件．（取g=10m/s2）
（2011?泰兴市模拟）在如图所示装置中，两物体质量分别为m1、m2，悬点a、b间的距离远大于滑轮的直径，不计一切摩擦，整个装置处于静止状态．由图可知（ ）
（2011?泰兴市模拟）物体m静止与斜面体M一起静止在水平面上．若将斜面的倾角A稍微增大一些，且物体m仍然静止在斜面上，则（ ）
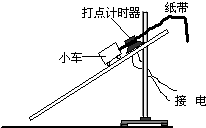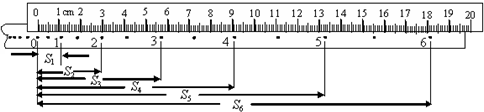
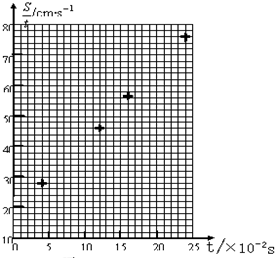
（2011?泰兴市模拟）某同学用图所示的实验装置研究小车在斜面上的运动．实验步骤如下：
