题目内容
1. 如图所示,y轴右方有方向垂直于纸面向里的匀强磁场,一个质量为m、电量为q的质子以速度V水平向右通过X轴上P点,最后从y轴上的M点射出磁场,已知M点到原点O的距离为H,质子射出磁场时速度方向与y轴负方向夹角θ=30°,(不计质子重力)求:
如图所示,y轴右方有方向垂直于纸面向里的匀强磁场,一个质量为m、电量为q的质子以速度V水平向右通过X轴上P点,最后从y轴上的M点射出磁场,已知M点到原点O的距离为H,质子射出磁场时速度方向与y轴负方向夹角θ=30°,(不计质子重力)求:(1)磁感应度的大小.
(2)适当的时候,在y轴右方再加一个匀强电场就可以使质子最终能沿y轴正方向做匀速直线运动.从质子经过P点开始计时,再经过多长时间加这个匀强电场?电场强度多大?方向如何?
分析 (1)由于磁场只存在x≥0区域,质子沿x轴正方向运动时,若洛伦兹力方向沿y轴负方向,则质子在第四象限运动,就不可能达M点,所以质子所受洛伦兹力方向必沿y轴正方向,再由左手定则判定磁场方向应垂直纸面向里.
(2)由题意和半径公式可知,要求磁感应强度B应先求半径R,要求半径得首先确定圆心.题中已知圆周上P、M两点的速度方向,可确定圆心O,根据几何关系和向心力公式即可求解.
解答 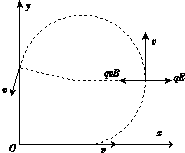 解:(1)质子在磁场中做匀速圆周运动
解:(1)质子在磁场中做匀速圆周运动
根据牛顿第二定律得:BqV=$\frac{{m{V^2}}}{r}$
如图根据几何知识得:H=r+rsin30°
所以磁感应强度的大小是B=$\frac{3mV}{2Hq}$
(2)质子的速度方向平行y轴沿y轴正方向时,所受洛伦兹力方向平行于X轴,指向X轴的负方向.这时沿平行于X轴的方向上加上适当的电场,可使质子受到的洛伦兹力和电场力平衡,使质子沿平行于y轴的正方向匀速直线运动.
则所用时间为:t=$\frac{1}{4}T$
而T=$\frac{2πm}{Bq}$
所以:t=$\frac{πm}{2Bq}$=$\frac{πH}{3V}$
质子匀速直线运动时有:BqV=Eq
得:E=BV=$\frac{{3m{V^2}}}{2Hq}$
因为质子带正电,所以电场强度的方向沿平行于X轴的正方向.
答:(1)磁感应度的大小为$\frac{3mV}{2Hq}$.
(2)适当的时候,在y轴右方再加一个匀强电场就可以使质子最终能沿y轴正方向做匀速直线运动.从质子经过P点开始计时,再经过$\frac{πH}{3V}$时间加这个匀强电场,电场强度大小为$\frac{3m{V}^{2}}{2Hq}$,方向沿平行于X轴的正方向.
点评 带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径,同时还利用圆弧的几何关系来帮助解题,难度适中.


| A. | 物块D受到一个大小为10的摩擦力 | |
| B. | 物块B受到水平桌面一个大小为10N的摩擦力 | |
| C. | C对B的压力大小为10N | |
| D. | OP绳产生的拉力为10$\sqrt{2}$N |
| A. | 惯性减小为$\frac{1}{6}$,重力不变 | B. | 惯性和重力都减小为$\frac{1}{6}$ | ||
| C. | 惯性不变,重力减小为$\frac{1}{6}$ | D. | 惯性和重力都不变 |
| A. | 同学甲用力把同学乙推倒,说明只是甲对乙有力的作用,乙对甲没有力的作用 | |
| B. | 电灯吊在电线下,灯对电线拉力的施力物体应该是地球 | |
| C. | 任何一个物体,一定既是受力物体,同时也是施力物体 | |
| D. | 球被一脚踢出后,在空中仍然受到一个向前的力 |
| A. | 可能做匀速直线运动 | B. | 可能做匀加速直线运动 | ||
| C. | 可能做匀速圆周运动 | D. | 一定做轨迹为抛物线的曲线运动 |
 在某电视台娱乐节目中,一选手从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度s0=1.2m.由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,选手经过反应时间△t=1.0s后,立刻以a=2m/s2恒定加速度向右跑至传送带最右端.已知重力加速度为g=10m/s2.若传送带以u=1m/s的恒定速度向左运动,选手要能到达传送带右端,他从高台上跃出的水平速度v至少多大?
在某电视台娱乐节目中,一选手从较高的平台上以水平速度跃出后,落在水平传送带上,已知平台与传送带高度差H=1.8m,水池宽度s0=1.2m.由于传送带足够粗糙,假设人落到传送带上后瞬间相对传送带静止,选手经过反应时间△t=1.0s后,立刻以a=2m/s2恒定加速度向右跑至传送带最右端.已知重力加速度为g=10m/s2.若传送带以u=1m/s的恒定速度向左运动,选手要能到达传送带右端,他从高台上跃出的水平速度v至少多大? 如图所示,左侧是倾角为60°的斜面,右侧是圆弧面的物体固定在水平地面上,圆弧面底端的切线水平,一根两端分别系有质量为m1、m2小球的轻绳跨过其顶点上的小滑轮.当它们处于平衡状态时,连接m2小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点.两小球的质量之比m1:m2为多少?
如图所示,左侧是倾角为60°的斜面,右侧是圆弧面的物体固定在水平地面上,圆弧面底端的切线水平,一根两端分别系有质量为m1、m2小球的轻绳跨过其顶点上的小滑轮.当它们处于平衡状态时,连接m2小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点.两小球的质量之比m1:m2为多少?