题目内容
9.某人手持边长为6cm的正方形平面镜测量身后一棵树的高度.测量时保持镜面与地面垂直,镜子与眼睛的距离为0.4m.在某位置时,他在镜中恰好能够看到整棵树的像;然后他向前走了6.0m,发现用这个镜子长度的$\frac{5}{6}$就能看到整棵树的像,求这个树的高度.(要求在答题卷上画出符合题意的光路图)分析 正确作出光路图,利用光路可逆,通过几何关系计算出树的高度.这是解决光路图题目的一般思路.
解答 解:设树高为H,树到镜的距离为L,如图所示,是恰好看到树时的反射光路图,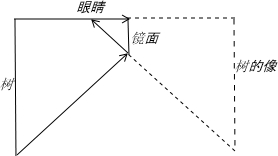
由图中的三角形可得
$\frac{树高}{镜高}$=$\frac{树到镜的距离+眼睛到镜的距离}{眼睛到镜的距离}$
即$\frac{H}{0.06}$=$\frac{L+0.4}{0.4}$.
人离树越远,视野越开阔,看到树的全部所需镜面越小,
同理有$\frac{H}{0.06×\frac{5}{6}}$=$\frac{L+0.4+6}{0.4}$,
以上两式解得:L=29.6m、H=4.5m.
答:这个树的高度4.5m.
点评 考查光的反射定律,掌握平面镜的反射成像,通常要正确的转化为三角形求解,注意画出正确的光路图.

练习册系列答案
相关题目
4. 汽车在水平面上向右匀速前进,汽车后挂钩上的绳子通过滑轮连接重物G,如图所示,若不计滑轮摩擦和绳子的质量,则绳子上的拉力( )
汽车在水平面上向右匀速前进,汽车后挂钩上的绳子通过滑轮连接重物G,如图所示,若不计滑轮摩擦和绳子的质量,则绳子上的拉力( )
 汽车在水平面上向右匀速前进,汽车后挂钩上的绳子通过滑轮连接重物G,如图所示,若不计滑轮摩擦和绳子的质量,则绳子上的拉力( )
汽车在水平面上向右匀速前进,汽车后挂钩上的绳子通过滑轮连接重物G,如图所示,若不计滑轮摩擦和绳子的质量,则绳子上的拉力( )| A. | 总是大于重物重力G,并逐渐减小 | |
| B. | 总是大于重物重力G,并逐渐增大 | |
| C. | 总是等于重物重力G | |
| D. | 先大于重物重力G,后逐渐减小并小于重力G |
4. 如图所示的同心圆是电场中的一簇等势线,一个电子只在电场力作用下沿着直线从A向C运动,运动的速度越来越小,B为线段AC的中点,则下列结论中正确的有( )
如图所示的同心圆是电场中的一簇等势线,一个电子只在电场力作用下沿着直线从A向C运动,运动的速度越来越小,B为线段AC的中点,则下列结论中正确的有( )
 如图所示的同心圆是电场中的一簇等势线,一个电子只在电场力作用下沿着直线从A向C运动,运动的速度越来越小,B为线段AC的中点,则下列结论中正确的有( )
如图所示的同心圆是电场中的一簇等势线,一个电子只在电场力作用下沿着直线从A向C运动,运动的速度越来越小,B为线段AC的中点,则下列结论中正确的有( )| A. | 电子沿AC运动时受到的电场力越来越小 | |
| B. | 电子沿AC运动时它具有的电势能越来越大 | |
| C. | 电势差UAB=UBC | |
| D. | 电势φA>φB>φC |
18.一辆汽车从原点O由静止出发沿x轴做直线运动,为研究汽车运动的规律而记录下它在不同时刻的位置和速度,见表所示.试求:
(1)汽车在3.5s末的速度和5.5s末的速度;
(2)前4s内的加速度.
| 时刻t/s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 位置坐标x/m | 0 | 0.5 | 2.0 | 4.4 | 8.0 | 12 | 16 | 20 |
| 瞬时速度v/(m•s-1) | 0 | 1 | 2 | 3 | 4 | 4 | 4 | 4 |
(2)前4s内的加速度.


 如图所示,两个完全相同的小球在挡板作用下静止在倾角为θ的光滑斜面上,甲挡板竖直,乙挡板与斜面垂直,求甲、乙两种情况下斜面对小球的支持力大小之比.
如图所示,两个完全相同的小球在挡板作用下静止在倾角为θ的光滑斜面上,甲挡板竖直,乙挡板与斜面垂直,求甲、乙两种情况下斜面对小球的支持力大小之比. 如图所示,y轴右方有方向垂直于纸面向里的匀强磁场,一个质量为m、电量为q的质子以速度V水平向右通过X轴上P点,最后从y轴上的M点射出磁场,已知M点到原点O的距离为H,质子射出磁场时速度方向与y轴负方向夹角θ=30°,(不计质子重力)求:
如图所示,y轴右方有方向垂直于纸面向里的匀强磁场,一个质量为m、电量为q的质子以速度V水平向右通过X轴上P点,最后从y轴上的M点射出磁场,已知M点到原点O的距离为H,质子射出磁场时速度方向与y轴负方向夹角θ=30°,(不计质子重力)求: 如图所示,在匀强电场中有a、b、c三点,a、b相距 4cm,b、c相距10cm.将一个带电荷量为2×10-6C的电荷从a点移到b点时,电场力做功为4×10-6 J.将此电荷从b点移到c点时电场力做功为5×10-6 J,a、c间电势差为450V.
如图所示,在匀强电场中有a、b、c三点,a、b相距 4cm,b、c相距10cm.将一个带电荷量为2×10-6C的电荷从a点移到b点时,电场力做功为4×10-6 J.将此电荷从b点移到c点时电场力做功为5×10-6 J,a、c间电势差为450V.