题目内容
1.在x轴上方有一匀强磁场,磁感应强度的方向垂直于纸面向里,大小为B,x轴下方有一匀强电场,电场强度的大小为E,方向与y轴的夹角θ为45°且斜向左上方(如图所示).现有一质量为m,电量为q的正离子,从y轴上的A点沿y轴正方向以初速度υ0开始运动,该离子在磁场中运动一段时间后从x轴上的C点进入电场区域,该离子经C点时的速度方向与x轴夹角为45°.不计离子的重力,设磁场区域和电场区域足够大.求:
(1)C点的坐标;
(2)离子从A点出发到第三次穿越x轴时的运动时间;
(3)离子第四次穿越x轴时速度的大小及速度方向与电场方向的夹角.
分析 (1)带电粒子在匀强磁场中在洛仑兹力作用下做匀速圆周运动,由牛顿第二定律求出轨迹半径.画出粒子运动的轨迹,由几何知识求出C点的坐标;
(2)根据运动轨迹的几何关系,来确定圆心角,并结合周期公式与牛顿第二定律、运动学公式,即可求解;
(3)根据粒子做类平抛运动处理规律,由运动的分解,并结合运动学公式,即可求解.
解答 解:(1)粒子运动轨迹如图所示: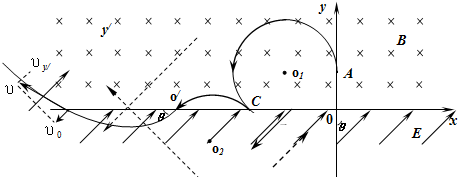
磁场中带电粒子在洛仑兹力作用下做匀速圆周运动,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$…①
粒子做圆周运动的周期:T=$\frac{2πr}{v}$=$\frac{2πm}{qB}$…②
由几何知识知:xC=-(r+rcos45°)=-$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$…③
故,C点坐标为(-$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$,0)…④
(2)设粒子从A到C的时间为t1,由题意知:t1=$\frac{5}{8}$T=$\frac{5πm}{4qB}$…⑤
设粒子从进入电场到返回C的时间为t2,其在电场中做匀变速运动,
由牛顿第二定律和运动学知识,有:
qE=ma…⑥2v0=at2…⑦
联立⑤⑥解得:t2=$\frac{2m{v}_{0}}{qE}$…⑧
设粒子再次进入磁场后在磁场中运动的时间为t3,由题意知:
t3=$\frac{1}{4}$T=$\frac{πm}{2qB}$…⑨
故粒子从A点到第三次穿越x轴的时间为:
t=t1+t2+t3=$\frac{7πm}{4qB}$+$\frac{2m{v}_{0}}{qE}$…⑩
(3)粒子从第三次过x轴到第四次过x轴的过程是在电场中做类似平抛的运动,沿着υ0的方向(设为x′轴)做匀速运动,即:
x′=v0t4 (11)vx′=v0 …(12)
沿着qE的方向(设为y′轴)做初速为0的匀变速运动,即:
y′=$\frac{1}{2}$$\frac{qE}{m}$t42…(13)vy′=$\frac{qE}{m}$t4 …(14)
设离子第四次穿越x轴时速度的大小为υ,速度方向与电场方向的夹角为α,
由图中几何关系知:tan45°=$\frac{y′}{x′}$…(15)
速度:v=$\sqrt{{v}_{0}^{2}+v{′}_{y}^{2}}$…(16)
tanα=$\frac{{v}_{0}}{{v}_{y}′}$…(17)
由(11)(12)(13)(14)(15)(16)(17)解得:
v=$\sqrt{5}$v0
α=arctan$\frac{1}{2}$;
答:(1)C点的坐标为(-$\frac{(2+\sqrt{2})m{v}_{0}}{2qB}$,0);
(2)离子从A点出发到第三次穿越x轴时的运动时间为$\frac{7πm}{4qB}$+$\frac{2m{v}_{0}}{qE}$;
(3)离子第四次穿越x轴时速度的大小为$\sqrt{5}$v0,速度方向与电场方向的夹角为arctan$\frac{1}{2}$.
点评 本题是粒子在电场和磁场中运动的问题,电场中类平抛运动的研究方法是运动的分解,磁场中圆周运动的研究方法是画轨迹.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | 不要在未放纸带时通电打点,每次打点完毕,应及时切断电源,切忌长时间通电使用 | |
| B. | 若发现振片振幅不稳定,应调节振片螺母,以使振动稳定 | |
| C. | 若打出的点带尾巴或双点,则是由于打点针太长所造成的,应适当调节打点针的长度 | |
| D. | 若打的点不清楚或有漏点,则检查复写纸是否已损坏或是否打点针太短 |
| A. | 气体吸收热量,内能减小 | B. | 气体吸收热量,内能增加 | ||
| C. | 气体放出热量,内能增加 | D. | 气体放出热量,内能减小 |
 如图所示,两相切圆表示一个静止的原子核发生衰变后的生成物在匀强磁场中的运动轨迹.由此可推知( )
如图所示,两相切圆表示一个静止的原子核发生衰变后的生成物在匀强磁场中的运动轨迹.由此可推知( )| A. | 原子核发生了α衰变 | B. | 原子核发生了β衰变 | ||
| C. | 原子核同时发生了α、β衰变 | D. | 该原子核放出一个中子 |
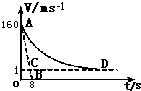 “神舟”五号飞船完成了预定空间科学和技术试验任务后,返回舱开始从太空向地球表面按预定轨道返回.返回舱开始时通过自身制动发动机进行调控变速下降,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降.这一过程中若返回舱所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k,所受空气浮力恒定不变,且认为竖直降落,从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示.图中AB是曲线AD在A点的切线,切线交于横轴一点B,其坐标为(8,0),CD是曲线AD的渐近线.假如返回舱总质量M=400kg,g取10m/s2.试问:
“神舟”五号飞船完成了预定空间科学和技术试验任务后,返回舱开始从太空向地球表面按预定轨道返回.返回舱开始时通过自身制动发动机进行调控变速下降,穿越大气层后,在一定的高度打开阻力降落伞进一步减速下降.这一过程中若返回舱所受空气阻力与速度的平方成正比,比例系数(空气阻力系数)为k,所受空气浮力恒定不变,且认为竖直降落,从某时刻开始计时,返回舱的运动v-t图象如图中的AD曲线所示.图中AB是曲线AD在A点的切线,切线交于横轴一点B,其坐标为(8,0),CD是曲线AD的渐近线.假如返回舱总质量M=400kg,g取10m/s2.试问: