题目内容
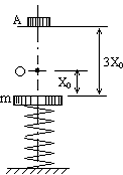
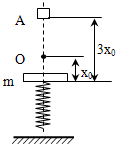 质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上,平衡时,弹簧的压缩量为x0,如图所示,一物块从钢板正上方距离为3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们到达最低点后又向上运动,已知物块质量也为m时,它们恰能回到O点,若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度,求物块向上运动到达最高点O点的距离.
质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上,平衡时,弹簧的压缩量为x0,如图所示,一物块从钢板正上方距离为3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们到达最低点后又向上运动,已知物块质量也为m时,它们恰能回到O点,若物块质量为2m,仍从A处自由落下,则物块与钢板回到O点时,还具有向上的速度,求物块向上运动到达最高点O点的距离.分析:分析物体的运动过程:物块先自由下落,机械能守恒.物块与钢板碰撞时,因碰撞时间极短,系统所受外力远小于相互作用的内力,遵守动量守恒定律.碰撞后,弹簧、物块与钢板组成的系统机械能守恒.由题碰撞后,物块与钢板回到O点时,此时弹簧的弹性势能与未碰撞时相等.根据动量守恒定律、机械能守恒定律和相等的条件分别研究物块质量为m和2m的情况,再求解物块向上运动到达最高点O点的距离.
解答:解:物块与钢板碰撞时的速度由机械能守恒,得
v0=
①
设v1表示质量为m的物块钢板碰撞后一起向下运动的速度,因碰撞时间极短,系统所受外力远小于相互作用的内力,符合动量守恒,故有
mv0=2mv1 ②
设刚碰完时弹簧的弹性势能为Ep,当他们一起回到O点时,弹簧无形变,弹簧势能为零,根据题意,由机械能守恒得
Ep+
(2m)
=2mgx0 ③
设v2表示质量为2m的物块与钢板碰后开始一起向下运动的速度,由动量守恒,则有
2mv0=3mv2 ④
设刚碰完时弹簧势能为Ep′,它们回到O点时,弹性势能为零,但它们仍继续向上运动,设此时速度为v2,则由机械能守恒定律得
+
(3m)
=3mgx0+
(3m)v2 ⑤
在上述两种情况下,弹簧的初始压缩量都是x0,故有Ep′=Ep ⑥
当质量为2m的物块与钢板一起回到O点时,弹簧的弹力为零,物块与钢板只受到重力的作用,加速度为g,一过O点,钢板受到弹簧向下的拉力作用,加速度大于g,由于物块与钢板不粘连,物块不可能受到钢板的拉力,其加速度仍为g,方向向下,故在O点物块与钢板分离.分离后,物块以速度v竖直上升,由竖直上抛最大位移公式得h=
,而v=
所以物块向上运动到达的最高点距O点的距离h=
.
v0=
| 6gx0 |
设v1表示质量为m的物块钢板碰撞后一起向下运动的速度,因碰撞时间极短,系统所受外力远小于相互作用的内力,符合动量守恒,故有
mv0=2mv1 ②
设刚碰完时弹簧的弹性势能为Ep,当他们一起回到O点时,弹簧无形变,弹簧势能为零,根据题意,由机械能守恒得
Ep+
| 1 |
| 2 |
| v | 2 1 |
设v2表示质量为2m的物块与钢板碰后开始一起向下运动的速度,由动量守恒,则有
2mv0=3mv2 ④
设刚碰完时弹簧势能为Ep′,它们回到O点时,弹性势能为零,但它们仍继续向上运动,设此时速度为v2,则由机械能守恒定律得
| E | / p |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
在上述两种情况下,弹簧的初始压缩量都是x0,故有Ep′=Ep ⑥
当质量为2m的物块与钢板一起回到O点时,弹簧的弹力为零,物块与钢板只受到重力的作用,加速度为g,一过O点,钢板受到弹簧向下的拉力作用,加速度大于g,由于物块与钢板不粘连,物块不可能受到钢板的拉力,其加速度仍为g,方向向下,故在O点物块与钢板分离.分离后,物块以速度v竖直上升,由竖直上抛最大位移公式得h=
| ||
| 2g |
| gx0 |
所以物块向上运动到达的最高点距O点的距离h=
| x0 |
| 2 |
点评:此题涉及的物理过程有四个,用到的物理规律和公式有四个,它将动量守恒和机械能守恒完美地统一在一起,交替使用,可以说是一道考查考生能力的好试题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目