题目内容
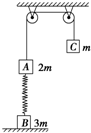 如图所示,质量为2m的物体A经一轻质弹簧与地面上的质量为3m的物体B相连,弹簧的劲度系数为k,一条不可伸长的轻绳绕过定滑轮,一端连物体A,另一端连一质量为m的物体C,物体A、B、C都处于静止状态.已知重力加速度为g,忽略一切摩擦.
如图所示,质量为2m的物体A经一轻质弹簧与地面上的质量为3m的物体B相连,弹簧的劲度系数为k,一条不可伸长的轻绳绕过定滑轮,一端连物体A,另一端连一质量为m的物体C,物体A、B、C都处于静止状态.已知重力加速度为g,忽略一切摩擦.(1)求物体B对地面的压力;
(2)把物体C的质量改为5m,这时C缓慢下降,经过一段时间系统达到新的平衡状态,这时B仍没离开地面,且C只受重力和绳的拉力作用,求此过程中物体A上升的高度.
分析:(1)以AB整体为研究对象,分析受力,求解地面对B的支持力,再求出B对地面的压力.
(2)以A为研究对象,先求出把物体C的质量改为5m时,弹簧的伸长量,再求出开始弹簧的压缩量,根据几何关系求出此过程中物体A上升的高度.
(2)以A为研究对象,先求出把物体C的质量改为5m时,弹簧的伸长量,再求出开始弹簧的压缩量,根据几何关系求出此过程中物体A上升的高度.
解答:解:
(1)对AB整体,根据平衡条件得:
mg+FN=5mg,
得地面对B的支持力FN=4mg,则物体B对地面的压力FN′=FN=4mg;
(2)对C:绳子的拉力FT=5mg.
对A:FT=Fk+2mg,
所以Fk=3mg,即kx1=3mg,
得到弹簧的伸长长度为x1=
开始时,弹簧的压缩量为x2,则
kx2=mg,
由几何关系得到,A上升的高度为:
hA=x1+x2=
.
解:
(1)物体B对地面的压力为4mg;
(2)此过程中物体A上升的高度为
.
(1)对AB整体,根据平衡条件得:
mg+FN=5mg,
得地面对B的支持力FN=4mg,则物体B对地面的压力FN′=FN=4mg;
(2)对C:绳子的拉力FT=5mg.
对A:FT=Fk+2mg,
所以Fk=3mg,即kx1=3mg,
得到弹簧的伸长长度为x1=
| 3mg |
| k |
开始时,弹簧的压缩量为x2,则
kx2=mg,
由几何关系得到,A上升的高度为:
hA=x1+x2=
| 4mg |
| k |
解:
(1)物体B对地面的压力为4mg;
(2)此过程中物体A上升的高度为
| 4mg |
| k |
点评:对于含有弹簧的问题,都要分析弹簧的状态,弹簧通常有三种状态:原长、伸长和压缩,根据几何关系研究物体上升的高度是常用的思路.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图所示,质量为2m的物块A与水平地面的动摩擦因数为μ,质量为m的物块B与地面的摩擦不计,在大小为F的水平推力作用下,A、B一起向右做加速运动,则A和B之间的作用力大小为( )
如图所示,质量为2m的物块A与水平地面的动摩擦因数为μ,质量为m的物块B与地面的摩擦不计,在大小为F的水平推力作用下,A、B一起向右做加速运动,则A和B之间的作用力大小为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,质量为2m和m的可看做质点的小球A、B,用不计质量不可伸长的细线相连,跨在固定的光滑圆柱两侧,开始时,A球和B球与圆柱轴心同高,然后释放A球,则B球到达最高点时速率是多少?
如图所示,质量为2m和m的可看做质点的小球A、B,用不计质量不可伸长的细线相连,跨在固定的光滑圆柱两侧,开始时,A球和B球与圆柱轴心同高,然后释放A球,则B球到达最高点时速率是多少? 如图所示,质量为2m的物块A和质量为m的物块B与地面的摩擦均不计,在已知水平恒力F的作用下,A、B一起做匀加速直线运动,则A对B的作用力大小为
如图所示,质量为2m的物块A和质量为m的物块B与地面的摩擦均不计,在已知水平恒力F的作用下,A、B一起做匀加速直线运动,则A对B的作用力大小为 如图所示,质量为2m的物块A和质量为m的物块B与地面的摩擦均不计.在已知水平推力F的作用下,A、B做加速运动.则由A和B组成的整体的加速度是
如图所示,质量为2m的物块A和质量为m的物块B与地面的摩擦均不计.在已知水平推力F的作用下,A、B做加速运动.则由A和B组成的整体的加速度是 如图所示,质量为2m的木板,静止放在光滑的水平面上,木板左端固定着一根轻质弹簧,一质量为m的小木块(大小不计)从木板右端以末知速度v0开始沿木板向左滑行,最终回到木板右端刚好末从木板右端刚好末从木板滑,若在小木块压缩弹簧过程中,弹簧具有最大弹性势能为Ep,小木块与木板间滑动摩擦力的大小保持不变,求未知速度v0的大小.
如图所示,质量为2m的木板,静止放在光滑的水平面上,木板左端固定着一根轻质弹簧,一质量为m的小木块(大小不计)从木板右端以末知速度v0开始沿木板向左滑行,最终回到木板右端刚好末从木板右端刚好末从木板滑,若在小木块压缩弹簧过程中,弹簧具有最大弹性势能为Ep,小木块与木板间滑动摩擦力的大小保持不变,求未知速度v0的大小.