题目内容
4. 如图所示,一内壁光滑的环形细圆管,由支架竖直支立在水平地面上.环形细圆管的环形半径为R(比细圆管的半径大得多).在环形细圆管中有A、B两小球(可视为质点)沿顺时针方向运动.设A、B两小球的质量均为m,环形细圆管的质量为2m,若A球以速率v1运动到最低点时,B球恰以速率v2运动到最高点,此刻支架对环形细圆管的支持力为mg.请导出v1与v2和R的关系式.
如图所示,一内壁光滑的环形细圆管,由支架竖直支立在水平地面上.环形细圆管的环形半径为R(比细圆管的半径大得多).在环形细圆管中有A、B两小球(可视为质点)沿顺时针方向运动.设A、B两小球的质量均为m,环形细圆管的质量为2m,若A球以速率v1运动到最低点时,B球恰以速率v2运动到最高点,此刻支架对环形细圆管的支持力为mg.请导出v1与v2和R的关系式.
分析 若A球以速率v1运动到最低点时,B球恰以速率v2运动到最高点时支架对环形细圆管有支持力,说明B球运动到最高点时对管道有向上的压力,管道对B球有向下的压力.根据牛顿第二定律分别对A、B球进行列式,再结合细管力平衡求解.
解答 解:据题,A球以速率v1运动到最低点时,B球恰以速率v2运动到最高点时支架对环形细圆管有支持力,则知B球运动到最高点时对管道有向上的压力,则管道对B球有向下的压力.
根据牛顿第二定律得:
对A球有:NA-mg=m$\frac{{v}_{1}^{2}}{R}$
对B球有:mg+NB=m$\frac{{v}_{2}^{2}}{R}$
据题分析有:NA-NB=mg
联立解得 ${v}_{2}^{2}-{v}_{1}^{2}$=gR
答:v1与v2和R的关系式为 ${v}_{2}^{2}-{v}_{1}^{2}$=gR.
点评 本题的关键是确定B球所受的弹力方向,再确定向心力的来源,由牛顿第二定律解答.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
19.竖直向上抛出一小球,3s末落回到抛出点,g取10m/s2,不计空气阻力.则( )
| A. | 小球抛出时的初速度是15m/s | |
| B. | 小球上升的最大高度是11.25m | |
| C. | 小球在第2秒内的位移是2.5m | |
| D. | 小球上升与下落过程加速度大小相等、方向相反 |
9. 在图示的电路中,电源电压不变.闭合电键K后,灯L1、L2都发光,-段时间后,其中的一盏灯突然变亮,而电压表Vl的示数变小,电压表V2的示数变大,则产生这一现象的原因是( )
在图示的电路中,电源电压不变.闭合电键K后,灯L1、L2都发光,-段时间后,其中的一盏灯突然变亮,而电压表Vl的示数变小,电压表V2的示数变大,则产生这一现象的原因是( )
 在图示的电路中,电源电压不变.闭合电键K后,灯L1、L2都发光,-段时间后,其中的一盏灯突然变亮,而电压表Vl的示数变小,电压表V2的示数变大,则产生这一现象的原因是( )
在图示的电路中,电源电压不变.闭合电键K后,灯L1、L2都发光,-段时间后,其中的一盏灯突然变亮,而电压表Vl的示数变小,电压表V2的示数变大,则产生这一现象的原因是( )| A. | 灯L1断路 | B. | 灯Ll短路 | C. | 灯L2断路 | D. | 灯L2短路 |
16.下列说法中正确的是( )
| A. | 布朗运动就是分子的无规则运动 | |
| B. | 多多晶体的物理性质表现为各向异性 | |
| C. | 只要外界对气体做了功,气体的内能就一定发生变化 | |
| D. | 物质由液态变为气态的过程,分子势能增大 |

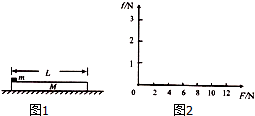 如图所示,质量M=2kg的木板静止在光滑的水平地面上,在木板的左端放置一个质量m=1kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ=0.2,取g=10m/s2,试求:
如图所示,质量M=2kg的木板静止在光滑的水平地面上,在木板的左端放置一个质量m=1kg、大小可以忽略的铁块,铁块与木板间的动摩擦因数μ=0.2,取g=10m/s2,试求: