题目内容
(20分)如图所示,AB为半径R=0.8m的1/4光滑圆弧轨道,下端B恰与小车右端平滑对接.小车质量M=3kg,车长L=2.06 m,车上表面距地面的高度h=0.2m.现有一质量m=1kg的滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5 s时,车被地面装置锁定.(g=10m/s2)试求:
(1)滑块到达B端时,轨道对它支持力的大小;
(2)车被锁定时,车右端距轨道B端的距离;
(3)从车开始运动到被锁定的过程中,滑块与车面间由于摩擦而产生的内能大小;
(4)滑块落地点离车左端的水平距离.
(1)30N (2)1m (3)6J (4)0.16m
解析试题分析:(1)设滑块到达B端时速度为v,
由动能定理,可得
由牛顿第二定律,可得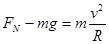
联立两式,解得轨道对滑块的支持力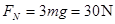
(2)当滑块滑上小车后,由牛顿第二定律,可得
对滑块: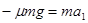
对小车:
设经时间t二者达到共同速度,则有: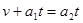
解得 ,由于
,由于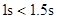 ,此时小车还未被锁定,
,此时小车还未被锁定,
两者的共同速度: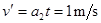
车被锁定时,车右端距轨道B端的距离: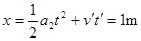
(3)从车开始运动到被锁定的过程中,滑块相对小车滑动的距离: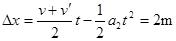
所以产生的内能:
(4)设滑块离开小车的速度为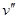
对滑块由动能定理,得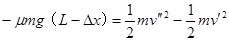
滑块脱离小车后,做平抛运动,在竖直方向有: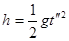
所以,滑块落地点离小车左端的水平距离:
联立以上各式,解得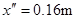
考点:本题考查了动能定理、匀变速直线运动和平抛运动规律的综合应用。

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 =37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1 s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10 m/s2.
=37°的固定且足够长的斜面上,对物体施以平行于斜面向上的拉力F,在t1=1 s时撤去拉力,物体运动的部分vt图象如图乙所示.重力加速度g取10 m/s2. 。试求:
。试求:

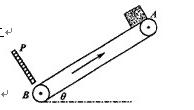
 =O.8 m,质量M=12 kg,在牵引力为零时,仍在向前运动。车与路面的动摩擦因数为O.3,当车速为
=O.8 m,质量M=12 kg,在牵引力为零时,仍在向前运动。车与路面的动摩擦因数为O.3,当车速为 =7 m/s时,把一个质量为m=1 kg的物体(可视为质点)轻轻地放在车顶前端,如图所示,问物体落地时,物体距车的前端有多远?(g=10m/s2)
=7 m/s时,把一个质量为m=1 kg的物体(可视为质点)轻轻地放在车顶前端,如图所示,问物体落地时,物体距车的前端有多远?(g=10m/s2)

 以内不会被甩出转盘,转盘的角速度ω应限制在什么范围?
以内不会被甩出转盘,转盘的角速度ω应限制在什么范围?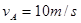 ,B车在后,其速度
,B车在后,其速度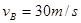 ,因大雾能见度低,B车在距A车
,因大雾能见度低,B车在距A车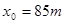 时才发现前方有A车,这时B车立即刹车,但B车要经过180
时才发现前方有A车,这时B车立即刹车,但B车要经过180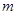 才能停止,问:B车刹车时A车仍按原速率行驶,两车是否会相撞?若会相撞,将在B车刹车后何时相撞?若不会相撞,则两车最近距离是多少?
才能停止,问:B车刹车时A车仍按原速率行驶,两车是否会相撞?若会相撞,将在B车刹车后何时相撞?若不会相撞,则两车最近距离是多少?