题目内容
2.机车在动摩擦因数μ1=0.2的平直水泥公路上匀速行驶的最大速度是V1,在动摩擦因数μ2=0.3的普通平直公路上行驶的最大速度是V2.则V1:V2=3:2;若关闭发动机在上述两种道路上,从最大行驶速度到停下来,分别前进的距离之比S1:S227:8.分析 汽车以恒定的功率匀速运动时,汽车受到的阻力的大小和汽车的牵引力的大小相等,由P=Fv可以求得最大速度关系.
关闭发动机在上述两种道路上,从最大行驶速度到停下来,根据动能定理列出等式进行比较.
解答 解:汽车以速度v1匀速运动时,
由P=Fv得
P=Fv1=fv1=μ1mgv1
汽车以速度v2运动时,
由P=Fv得
P=F′v2=f′v2=μ2mgv2
所以v1:v2=μ2:μ1=3:2.
若关闭发动机在上述两种道路上,从最大行驶速度到停下来,根据动能定理得:
-fS=0-$\frac{1}{2}$mv2
S=$\frac{m{v}^{2}}{2f}$
所以s1:s2=$\frac{\frac{{3}^{2}}{2}}{\frac{{2}^{2}}{3}}$=27:8
故答案为:3:2,27:8
点评 解决本题的关键知道发动机的功率与牵引力和速度的关系,知道在平直公路上,牵引力与阻力相等时,速度最大.

练习册系列答案
相关题目
13.对曲线运动的速度,下列说法正确的是( )
| A. | 速度的大小与方向一定都在时刻变化 | |
| B. | 速度的大小不断发生变化,速度的方向不一定发生变化 | |
| C. | 速度的方向不断发生变化,速度的大小不一定发生变化 | |
| D. | 质点在某一点的速度方向不一定是曲线在这一点的切线方向 |
17.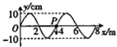 一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )
一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )
 一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )
一列简谐横波沿x轴方向传播,某时刻的波形如图所示,波的传播速度v=10m/s,此时P点的振动方向沿y轴负方向,下说法正确的是( )| A. | 该波沿x轴正方向传播 | |
| B. | 该波的振幅为20cm | |
| C. | 该波的周期为0.4s | |
| D. | 从该时刻起再过0.7s,P点到达波峰的位置 | |
| E. | 从该时刻起再过0.6s,P点沿波的传播方向前进了6m |
7.下列关于质点的说法,正确的是( )
| A. | 体积很小的物体都可以看成质点 | |
| B. | 若物体的大小、形状对所研究的问题无影响,则该物体可看成质点 | |
| C. | 匀速运动的火车一定可视为质点 | |
| D. | 研究乒乓球的旋转时乒乓球可视为质点 |
11.学过单摆的周期公式以后,物理兴趣小组的同学们对钟摆产生了兴趣,老师建议他们先研究用厚度和质量分布均匀的方木块(如一把米尺)做成的摆(这种摆被称为复摆),如图1所示.让其在竖直平面内做小角度摆动,C点为重心,板长为L,周期用T表示.
甲同学猜想:复摆的周期应该与板的质量有关.
乙同学猜想:复摆的摆长应该是悬点到重心的距离$\frac{L}{2}$.
丙同学猜想:复摆的摆长应该大于$\frac{L}{2}$.理由是:若OC段看成细线,线栓在C处,C点以下部分的重心离O点的距离显然大于$\frac{L}{2}$.
为了研究以上猜想是否正确,同学们进行了下面的实验探索:

(1)把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点.则证明了甲同学的猜想是错误的(选填“正确”或“错误”).
(2)用T0表示板长为L的复摆看成摆长为$\frac{L}{2}$单摆的周期计算值(T0=2π$\sqrt{\frac{\frac{L}{2}}{g}}$),用T表示板长为L复摆的实际周期测量值.计算与测量的数据如表:
由上表可知,复摆的等效摆长大于$\frac{L}{2}$(选填“大于”、“小于”或“等于”).
(3)为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标如图2.请在坐标纸上作出T-T0图,并根据图象中反映出的规律求出$\frac{\sqrt{{L}_{等}}}{\sqrt{\frac{L}{2}}}$=1.1(结果保留三位有效数字,其中L等是板长为L时的等效摆长T=2$π\sqrt{\frac{L_等}{g}}$).
甲同学猜想:复摆的周期应该与板的质量有关.
乙同学猜想:复摆的摆长应该是悬点到重心的距离$\frac{L}{2}$.
丙同学猜想:复摆的摆长应该大于$\frac{L}{2}$.理由是:若OC段看成细线,线栓在C处,C点以下部分的重心离O点的距离显然大于$\frac{L}{2}$.
为了研究以上猜想是否正确,同学们进行了下面的实验探索:

(1)把两个相同的木板完全重叠在一起,用透明胶(质量不计)粘好,测量其摆动周期,发现与单个木板摆动时的周期相同,重做多次仍有这样的特点.则证明了甲同学的猜想是错误的(选填“正确”或“错误”).
(2)用T0表示板长为L的复摆看成摆长为$\frac{L}{2}$单摆的周期计算值(T0=2π$\sqrt{\frac{\frac{L}{2}}{g}}$),用T表示板长为L复摆的实际周期测量值.计算与测量的数据如表:
| 板长L/cm | 25 | 50 | 80 | 100 | 120 | 150 |
| 周期计算值T0/s | 0.70 | 1.00 | 1.27 | 1.41 | 1.55 | 1.73 |
| 周期测量值T/s | 0.81 | 1.16 | 1.47 | 1.64 | 1.80 | 2.01 |
(3)为了进一步定量研究,同学们用描点作图法对数据进行处理,所选坐标如图2.请在坐标纸上作出T-T0图,并根据图象中反映出的规律求出$\frac{\sqrt{{L}_{等}}}{\sqrt{\frac{L}{2}}}$=1.1(结果保留三位有效数字,其中L等是板长为L时的等效摆长T=2$π\sqrt{\frac{L_等}{g}}$).
 如图所示,真空中有一对相距为d的平行金属板A和B,两板间电势差为U,两板间的电场为匀强电场.若一个质量为m、电荷量为q的粒子,仅在静电力的作用下由静止开始从A板向B板做匀加速直线运动并到达B板,则
如图所示,真空中有一对相距为d的平行金属板A和B,两板间电势差为U,两板间的电场为匀强电场.若一个质量为m、电荷量为q的粒子,仅在静电力的作用下由静止开始从A板向B板做匀加速直线运动并到达B板,则 图为一正在测量中的多用电表表盘.
图为一正在测量中的多用电表表盘. 一光滑的小球从斜面顶端由静止开始匀加速滑到底端,已知小球在后半段所用时间为5s,求前半段时间为多少?(注:本题不能用比例推论来做)
一光滑的小球从斜面顶端由静止开始匀加速滑到底端,已知小球在后半段所用时间为5s,求前半段时间为多少?(注:本题不能用比例推论来做)