题目内容
已知一列沿x轴正向传播的简谐横波t=0时刻波形图如图所示,且波刚好传到A点,振幅为5m。再经过1.1s时,x=1m处的P质点第3次出现波峰,求:
(1)波速v=?
(2)从t=0至t=1.2s,质点P运动的路程L是多少?t=1.2s时,质点P的位移y是多少?
(3)由图示时刻起,x=6m处的Q点再经过多长时间第一次出现波峰?
(1)10m/s;(2)60m;0;(3)0.4s。
解析试题解析:(1)由于波长为λ=4m,且再经过1.1s时,x=1m处的P质点第3次出现波峰,说明该质点经过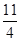 T所用的时间为1.1s,因为质点在t=0时的振动方向沿y轴的负方向;故得周期T=0.4s,则波速v=
T所用的时间为1.1s,因为质点在t=0时的振动方向沿y轴的负方向;故得周期T=0.4s,则波速v=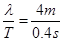 ="10" m/s;
="10" m/s;
(2)由于周期为0.4s,故从t=0至t=1.2s,质点经过了3个周期,每个周期质点的路程为4A,则质点P运动的路程L=3×4A=12×5m=60m;由于质点经过3个周期后又回到了原来的位置,故位移的大小为0。
(3)由于波的传播方向是沿x轴的正方向,故振源的振动方向是向下的,从t=0时刻波传播到Q点的时间为t1= =0.1s,且向下振动,故要经过
=0.1s,且向下振动,故要经过 个周期才能第一次出现波峰,所以这段时间为t2=0.3s,所以总时间为0.1s+0.3s=0.4s。
个周期才能第一次出现波峰,所以这段时间为t2=0.3s,所以总时间为0.1s+0.3s=0.4s。
考点:波的传播方向与振动方向的关系,波速的计算,周期的识别等。

一列简谐横波沿x轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.6s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是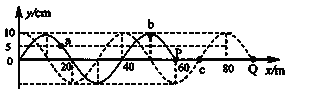
| A.这列波的波速可能为50m/s |
| B.质点a在这段时间内通过的路程一定小于30cm |
C.若周期T=0.8s,当t+0.4s时刻开始计时,则质点c的振动方程为 m m |
| D.若周期T=0.8s,则当t+0.5s时刻,质点b的位移小于P的位移 |
如图所示,a是一列正弦波在t=0时刻的波形曲线,P是波形曲线上的一个质点.b是t=0.4 s时的波形曲线.
(1)求这列波的波速;
(2)若这列波是沿x轴负方向传播的,试说出质点P在t=0时刻的运动方向.
两列振动方向相同、振幅分别为A1和A2的相干简谐横波相遇。下列说法正确的是( )
| A.波峰与波谷相遇处质点的振幅为|A1-A2| |
| B.波峰与波峰相遇处质点离开平衡位置的位移始终为A1+A2 |
| C.波峰与波谷相遇处质点的位移总是小于波峰与波峰相遇处质点的位移 |
| D.波峰与波峰相遇处质点的振幅一定大于波峰与波谷相遇处质点的振幅 |
(6分)如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2 m和x=1.2 m处,两列波的速度均为v=0.4 m/s,两波源的振幅均为A=2 cm。图示为t=0时刻两列波的图像(传播方向如图所示),此刻平衡位置处于x=0.2 m和x=0.8 m的P、Q两质点刚开始振动。质点M的平衡位置处于x=0.5 m处,关于各质点运动情况判断正确的是( )(填正确答案标号。选对1个得2分,选对2个得4分,选对3个得6分;每选错1个扣3分,最低得分为0分)
| A.两列波相遇后振幅仍然为2cm |
| B.t=1 s时刻,质点M的位移为-4 cm |
| C.t=1 s时刻,质点M的位移为+4 cm |
| D.t=0.75 s时刻,质点P、Q都运动到M点 |
如图所示,一简谐横波在x轴上传播,轴上a、b两点相距12m.t=0时a点为波峰,b点为波谷;t=0.5s时a点为波谷,b点为波峰,则下列判断只正确的是 ( )
| A.波一定沿x轴正方向传播 |
| B.波长可能是8m |
| C.周期可能是0.5s |
| D.波速一定是24m/s |
(6分)如图所示,Sl、S2为两个振动情况完全一样的波源,两列波的波长都为 ,它们在介质中产生干涉现象,Sl、S2在空间共形成了5个振动加强的区域,如图中实线所示。P是振动加强区域中的一点,从图中可看出
,它们在介质中产生干涉现象,Sl、S2在空间共形成了5个振动加强的区域,如图中实线所示。P是振动加强区域中的一点,从图中可看出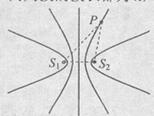
A.P点到两波源的距离差等于1.5 |
| B.S1的传播速度大于S2的传播速度 |
| C.P点此时刻振动最强,过半个周期后,振动变为最弱 |
| D.当一列波的波峰传到P点时,另一列波的波峰也一定传到P点 |

