题目内容
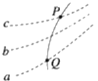
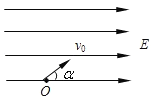
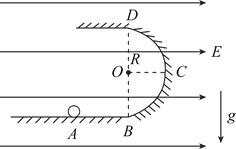
【题目】如图所示,![]() 为表示竖立放在场强为
为表示竖立放在场强为![]() 的水平匀强电场中的绝缘光滑轨道,其中轨道的
的水平匀强电场中的绝缘光滑轨道,其中轨道的![]() 部分是半径为
部分是半径为![]() 的半圆环,轨道的水平部分与半圆环相切
的半圆环,轨道的水平部分与半圆环相切![]() 为水平轨道的一点,而且
为水平轨道的一点,而且![]() ,把一质量
,把一质量![]() 、带电
、带电![]() 的小球,放在水平轨道的
的小球,放在水平轨道的![]() 点上面由静止开始被释放后,在轨道的内侧运动.(
点上面由静止开始被释放后,在轨道的内侧运动.(![]() )求:
)求:
(1)它到达![]() 点时的速度是多大?
点时的速度是多大?
(2)它到达![]() 点时对轨道压力是多大?
点时对轨道压力是多大?
(3)小球所能获得的最大动能是多少?
【答案】(1)2m/s(2)3N(3)![]()
【解析】
(1)题的关键是可以应用动能定理直接求出速度;(2)题关键是应用牛顿第二定律可求压力;(3)题的关键是首先找到动能最大的位置即所谓“等效最低点”的方法,即小球能够平衡的位置,然后结合动能定理即可求解.
(1)设小球在C点的速度大小是![]() ,则对于小球由A→C的过程中,由动能定律得:
,则对于小球由A→C的过程中,由动能定律得:![]()
解得:![]()
(2)小球在C点时受力分析如图

由牛顿第二定律有:![]()
解得![]()
由牛顿第三定律可知小球对轨道的压力为3N.
(3)由mg=qE=1N,可知小球受到合力的方向垂直于B、C点的连线BC指向圆心O,所以“等效最低点”在BC的中点E,设小球的最大动能为![]()
由动能定理可得:![]()
解得:![]()

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目