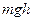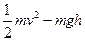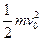题目内容
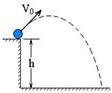
如图所示,小球A从半径为R=0.8 m的1/4光滑圆弧轨道的上端点以v0=3 m/s的初速度开始滑下,到达光滑水平面上以后,与静止于该水平面上的钢块B发生碰撞,碰撞后小球A被反向弹回,沿原路进入轨道运动恰能上升到它下滑时的出发点(此时速度为零).设A、B碰撞机械能不损失,g取10 m/s2,求:
(1)小球A刚滑上水平面的速度.
(2)A和B的质量之比.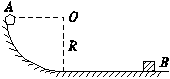
(1)小球A刚滑上水平面的速度.
(2)A和B的质量之比.

(1)设小球A刚滑上水平面的速度为vA,应用机械能守恒可得:
mv+mgR=mv vA==5 m/s.
(2)设A、B相碰后的速度大小分别为vA′、vB′,由题意可知:mvA′2=mgR,得vA′=4 m/s
由碰撞过程中的动量、动能均守恒可得mAvA=mBvB′-mAvA′
mAv=mBvB′2+mAvA′2
代入数据可联立求出mA∶mB=1∶9.
mv+mgR=mv vA==5 m/s.
(2)设A、B相碰后的速度大小分别为vA′、vB′,由题意可知:mvA′2=mgR,得vA′=4 m/s
由碰撞过程中的动量、动能均守恒可得mAvA=mBvB′-mAvA′
mAv=mBvB′2+mAvA′2
代入数据可联立求出mA∶mB=1∶9.
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 mv02
mv02 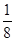 mv02
mv02 mv02
mv02

 的木板DF,F端在轨道最高点C的正下方,竖直距离为5cm。水平轨道的另一端B处有一质量m
的木板DF,F端在轨道最高点C的正下方,竖直距离为5cm。水平轨道的另一端B处有一质量m 2=0.2kg的小球,m1、m2两小球在B处发生的是完全弹性碰撞,重力加速度为g=10m/s2. 求:
2=0.2kg的小球,m1、m2两小球在B处发生的是完全弹性碰撞,重力加速度为g=10m/s2. 求:
 放一质量为m的小木块A,m<M。现以地面为参考系,给A和B以大小相同,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。求小木块A向左运动到达最远处(对地)离出发点的距离。
放一质量为m的小木块A,m<M。现以地面为参考系,给A和B以大小相同,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。求小木块A向左运动到达最远处(对地)离出发点的距离。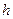 处以初速度
处以初速度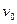 抛出一个质量为
抛出一个质量为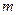 的物体,物体落地时速度为
的物体,物体落地时速度为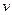 ,不计空气阻力,取抛出位置所在水平面为零势能面,则物体着地时的机械能为( )
,不计空气阻力,取抛出位置所在水平面为零势能面,则物体着地时的机械能为( )