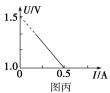
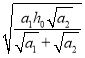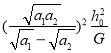题目内容
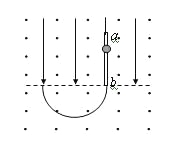
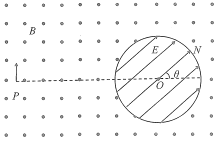
【题目】如图,在纸面内有一圆心为O、半径为R的圆,圆形区域内存在斜向上的电场,电场强度大小未知,区域外存在垂直于纸面向外的匀强磁场,磁感应强度大小为B,一质量为m、电荷量为q的正粒子从圆外P点在纸面内垂直于OP射出,已知粒子从Q点(未画出)进入圆形区域时速度垂直Q点的圆弧切线,随后在圆形区域内运动,并从N点(ON连线的方向与电场方向一致,ON与PO的延长线夹角![]() )射出圆形区域,不计粒子重力,已知OP=3R
)射出圆形区域,不计粒子重力,已知OP=3R
(1)求粒子第一次在磁场中运动的速度大小;
(2)求电场强度和粒子射出电场时的速度大小。
【答案】(1)![]() ;(2)
;(2) ![]() ,
,![]()
【解析】
(1)根据题意,画出粒子在磁场中运动的轨迹,如图所示:
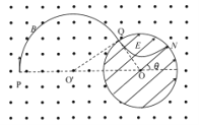
设粒子在磁场中做圆周运动的半径为r,由几何关系有
![]()
解得
![]()
由洛伦兹力提供向心力有
![]()
解得
![]()
(2)因为QO与PO的夹角为53°,所以入射速度与电场垂直,也就是带电粒子在电场中做类平抛运动,又因为从N点射出,所以有
![]()
![]()
又
qE=ma
解得
![]() ,
,![]()
由动能定理有
![]()
可得
![]()

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目