Question

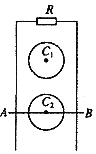
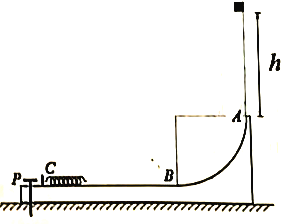
【题目】如图所示，一工件用锁定装置固定于光滑水平面上，其段是一半径为的光滑圆弧轨道，段为粗糙水平轨道，二者相切于点，整个轨道处于同一竖直平面内，在处固定一根处于自然状态的轻质弹簧。一可视为质点的物块，其质量为，在点正上方某处由静止释放，从点进入轨道，已知工件的质量，重力加速度为。

(1)若释放高度，求物块第一次经过点时的速度的大小；

(2)解除锁定装置，若释放高度，物块第一次压缩弹簧后恰好能返回到轨道上的点处，设弹簧始终在弹性限度内，则此过程中求：

①弹簧的最大弹性势能；

②物块返回点的途中，在圆轨道上的点处受到的支持力的大小。

Answer 1

【答案】(1) (2) ① ②

【解析】

(1)物块由静止释放到达点，由动能定理得

（2）①物块从静止释放到第一次将弹簧压缩到最短时，物块与工件达到共同速度，由水平方向动量守恒可知，共同速度为0，由能量守恒定律得：

物块从静止释放到第一次压缩弹簧后返回到轨道上的点时，物块与工件达到共同速度，同样可知共同速度为0，由能量守恒定律得：

联立解得：

②物块第一次压缩弹簧返回到轨道上的点的途中，当物块经过点时，设物块和工件的速度大小分别为和，由系统水平方向动量守恒得

由能量守恒定律得：

联立解得：

物块在点时由支持力和重力的合力提供向心力

解得