题目内容
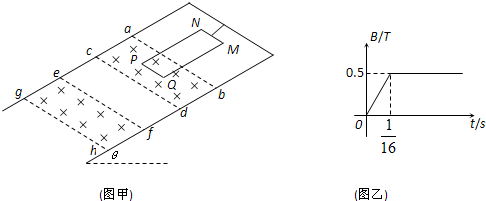
20. 如图所示,固定在水平面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时,adeb构成一个边长为l的正方形.棒的电阻为r,其余部分电阻不计.开始时磁感应强度为B0.
如图所示,固定在水平面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时,adeb构成一个边长为l的正方形.棒的电阻为r,其余部分电阻不计.开始时磁感应强度为B0.(1)若从t=0时刻起,磁感应强度均匀增加,每秒增量为k,同时保持静止.求棒中的感应电流,并说明方向.
(2)在上述(1)情景中,始终保持棒静止,当t=t1s末时需加的垂直于棒的水平拉力为多大?
分析 (1)根据法拉第电磁感应定律求解感应电动势大小,再由欧姆定律求出感应电流的大小,由楞次定律判断其方向.
(2)磁感应强度B的表达式为B=B0+kt,由安培力公式F=BIL求出安培力,则由平衡条件得知,水平拉力与安培力大小相等.
解答 解:(1)由题得:磁感应强度B的变化率为:△B△t△B△t=k T/s
由法拉第电磁感应定律知感应电动势为:E=△Φ△t△Φ△t=△B△t△B△tl2=kl2;
感应电流为:I=ErEr=kl2rkl2r
根据楞次定律知棒中感应电流方向为b→a.
(2)当t=t1时,B=B0+kt1
安培力大小为:F安=BIl
棒的水平拉力为:F=F安=(B0+kt1)kl3r(B0+kt1)kl3r
答:(1)棒中的感应电流大小为kl2rkl2r,方向为b→a.
(2)当t=t1s末时需加的垂直于棒的水平拉力为(B0+kt1)kl3r(B0+kt1)kl3r.
点评 本题根据法拉第电磁感应定律求解感应电动势,由欧姆定律和安培力公式推导安培力的表达式,是常用的方法和思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.从地面竖直上抛一个质量为m的小球,小球上升的最大高度为H,设上升过程中空气阻力f大小恒定,则在上升过程中下列说法中错误的是( )
| A. | 小球的加速度大于重力加速度g | B. | 小球的机械能减小了fH | ||
| C. | 小球的重力势能增加了mgH | D. | 小球的动能减小了mgH |
12.放射性元素2349023490Th的衰变方程为2349023490Th→2349123491Pa+X,下列表述正确的是( )
| A. | X是由Th原子释放的核外电子 | B. | 该衰变是β衰变 | ||
| C. | 若加压或加温则将衰变得更快 | D. | Th发生衰变时原子核要吸收能量 |
9.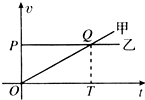 甲乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为s1和s2(s1=s2).初始时,甲车在乙车前方S0处.( )
甲乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为s1和s2(s1=s2).初始时,甲车在乙车前方S0处.( )
 甲乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为s1和s2(s1=s2).初始时,甲车在乙车前方S0处.( )
甲乙两车在一平直道路上同向运动,其v-t图象如图所示,图中△OPQ和△OQT的面积分别为s1和s2(s1=s2).初始时,甲车在乙车前方S0处.( )| A. | 若s0=s1+s2,两车不会相遇 | B. | 若s0<s1,两车相遇2次 | ||
| C. | 若s0=s1,两车相遇1次 | D. | 若s0=s2,两车相遇1次 |
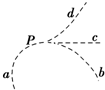 一质点以水平向右的恒定速度通过P点时受到一个恒力F的作用,则此后该质点的运动轨迹不可能是图中的( )
一质点以水平向右的恒定速度通过P点时受到一个恒力F的作用,则此后该质点的运动轨迹不可能是图中的( )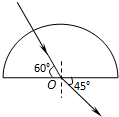 如图所示,一束单色光射向半圆玻璃砖的圆心O,入射光线与底边的夹角为60°,折射光线与底边的夹角为45°,已知真空中光速为c,求这束光在玻璃砖中的传播速度v.
如图所示,一束单色光射向半圆玻璃砖的圆心O,入射光线与底边的夹角为60°,折射光线与底边的夹角为45°,已知真空中光速为c,求这束光在玻璃砖中的传播速度v.