题目内容
10.通过理论分析可得出弹簧的弹性势能公式Ep=$\frac{1}{2}$kl2(式中k为弹簧的劲度系数,l为弹簧长度的变化量).为验证这一结论,A、B两位同学设计了以下的实验:
①两位同学首先都进行了如图甲所示的实验:将一根轻质弹簧竖直挂起,在弹簧的另一端挂上一个已知质量为m的小铁球,稳定后测得弹簧伸长d.
②A同学完成步骤①后,接着进行了如图乙所示的实验:将这根弹簧竖直地固定在水平桌面上,并把小铁球放在弹簧上,然后竖直地套上一根带有插销孔的长透明塑料管,利用插销压缩弹簧.拔掉插销时,弹簧对小球做功,使小球弹起,测得弹簧的压缩量l和小铁球上升的最大高度H.
③B同学完成步骤①后,接着进行了如图丙所示的实验:将这根弹簧放在水平桌面上,一端固定在竖直墙上,另一端被小铁球压缩,测得压缩量为l,释放弹簧后,小铁球从高为h的桌面上水平抛出,抛出的水平距离为x.
(1)A、B两位同学进行图甲所示的实验目的是为了确定什么物理量?请用m、d、g表示所求的物理量确定弹簧的劲度系数k.
(2)如果Ep=$\frac{1}{2}$kx2成立,
A同学测出的物理量x与d、H的关系式是:x=$\sqrt{2dH}$.
B同学测出的物理量x与d、h、L的关系式是:x=$L\sqrt{\frac{d}{2h}}$.
分析 (1)根据重力与弹簧的弹力平衡,借助于胡克定律,即可求解;
(2)A同学运用弹簧的弹性势能转化为重力势能来测量形变量,而B同学则是运用弹簧的弹性势能转化为动能,并借助于做平抛运动来算出初速度,从而即可求解;
解答 解:(1)A、B两位同学进行图甲所示的实验都进行形变量的测量,目的是为了确定弹簧的劲度系数;根据胡克定律$k=\frac{mg}{△x}$,则有:$k=\frac{mg}{d}$;
(2)A同学实验中,根据弹簧的弹性势能转化为重力势能,
则有:$\frac{1}{2}k{x}^{2}=mgH$
$k=\frac{mg}{d}$,
由上解得:$x=\sqrt{2dH}$
B同学,弹簧的弹性势能转化为动能,而动能则借助于平抛运动来测得初速度.
则由水平位移与竖直高度可得水平初速度:${v}_{0}=\frac{L}{\sqrt{\frac{2h}{g}}}=L\sqrt{\frac{g}{2h}}$,
所以:$\frac{1}{2}k(\frac{mg}{d})^{2}=\frac{1}{2}m(L\sqrt{\frac{g}{2h}})^{2}$
解得:$x=L\sqrt{\frac{d}{2h}}$
故答案为:(1)确定弹簧的劲度系数k;$k=\frac{mg}{d}$
(2)$\sqrt{2dH}$;$L\sqrt{\frac{d}{2h}}$
点评 本题考查如何测量弹簧的形变量,并通过不同的实验去设计、测量,并处理数据,最后数据误差分析,从而激发学生的学习兴趣.

练习册系列答案
相关题目
2. 如图所示,长0.5m的轻质细杆,一端固定有一个质量为3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球通过最高点时,对杆的弹力大小是24N.取g=10m/s2,小球的速度的大小是多少( )
如图所示,长0.5m的轻质细杆,一端固定有一个质量为3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球通过最高点时,对杆的弹力大小是24N.取g=10m/s2,小球的速度的大小是多少( )
 如图所示,长0.5m的轻质细杆,一端固定有一个质量为3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球通过最高点时,对杆的弹力大小是24N.取g=10m/s2,小球的速度的大小是多少( )
如图所示,长0.5m的轻质细杆,一端固定有一个质量为3kg的小球,另一端由电动机带动,使杆绕O点在竖直平面内做匀速圆周运动,小球通过最高点时,对杆的弹力大小是24N.取g=10m/s2,小球的速度的大小是多少( )| A. | 2m/s | B. | 3m/s | C. | 4m/s | D. | 1m/s |
20. 如图所示,表示两列相干水波的叠加情况,图中实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,波速和波长均为1m/s和0.5m,C点是BD连线的中点,下列说法中正确的是( )
如图所示,表示两列相干水波的叠加情况,图中实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,波速和波长均为1m/s和0.5m,C点是BD连线的中点,下列说法中正确的是( )
 如图所示,表示两列相干水波的叠加情况,图中实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,波速和波长均为1m/s和0.5m,C点是BD连线的中点,下列说法中正确的是( )
如图所示,表示两列相干水波的叠加情况,图中实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,波速和波长均为1m/s和0.5m,C点是BD连线的中点,下列说法中正确的是( )| A. | C点保持静止不动 | |
| B. | 图示的A、B两点的竖直高度差为20cm | |
| C. | 图示时刻C点正处在平衡位置且向下运动 | |
| D. | 从图示时刻起经0.25s后,B点通过的路程为20cm |
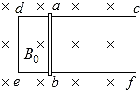 如图所示,固定在水平面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时,adeb构成一个边长为l的正方形.棒的电阻为r,其余部分电阻不计.开始时磁感应强度为B0.
如图所示,固定在水平面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时,adeb构成一个边长为l的正方形.棒的电阻为r,其余部分电阻不计.开始时磁感应强度为B0. 如图所示,用一根不可伸长的细绳将小球悬挂在O点做成单摆,绳长为1m.现将小球拉至A点释放,θ=60°,小球运动到B点的速度为3m/s.已知小球的质量为0.2kg,g取10m/s2.求:
如图所示,用一根不可伸长的细绳将小球悬挂在O点做成单摆,绳长为1m.现将小球拉至A点释放,θ=60°,小球运动到B点的速度为3m/s.已知小球的质量为0.2kg,g取10m/s2.求: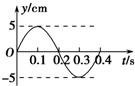 一简谐横波沿x轴正方向传播,若在x=1m处质点的振动图象如图所示,则该波在t=0.3s时刻的波形曲线为( )
一简谐横波沿x轴正方向传播,若在x=1m处质点的振动图象如图所示,则该波在t=0.3s时刻的波形曲线为( )



 如图所示,匀强电场中A、B、C三点构成一个直角三角形,∠A=30°,BC两点距离为2cm.电场线方向平行于△ABC所在平面.把电荷量q1=3×10-10C的正电荷由A点移动到B点,电场力做功4.8×10-8J,若将另一个电荷量为q2=1×10-10C的正电荷由B点移动到C点,电荷克服电场力做功1.6×10-8J,取B点的电势为零,求
如图所示,匀强电场中A、B、C三点构成一个直角三角形,∠A=30°,BC两点距离为2cm.电场线方向平行于△ABC所在平面.把电荷量q1=3×10-10C的正电荷由A点移动到B点,电场力做功4.8×10-8J,若将另一个电荷量为q2=1×10-10C的正电荷由B点移动到C点,电荷克服电场力做功1.6×10-8J,取B点的电势为零,求