题目内容
【题目】摩天大楼中一部高层的客运电梯,电梯的简化模型如图1所示.电梯的加速度a是随时间t变化的,已知电梯在t=0时由静止开始上升,a─t图象如图2所示.电梯总质量m=2.0×103kg.忽略一切阻力,重力加速度g取10m/s2 . 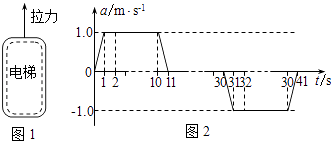
(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2;
(2)求电梯在匀速上升的过程中上升的高度是多少?
【答案】
(1)解:由牛顿第二定律,有 F﹣mg=ma,由a─t图象可知,F1和F2对应的加速度分别是:
a1=1.0m/s2,a2=﹣1.0m/s2则:
F1=m(g+a1)=2.0×103×(10+1.0)N=2.2×104N
F2=m(g+a2)=2.0×103×(10﹣1.0)N=1.8×104N
答:电梯在上升过程中受到的最大拉力F1是2.2×104N,最小拉力F2是1.8×104N
(2)解:通过类比可得,电梯的速度变化量等于a─t图线下的面积,第11s末的速率
υ11= ![]() =10m/s
=10m/s
11s﹣30s电梯做匀速上升:h=υ11t=10×19=190m
答:电梯在匀速上升的过程中上升的高度是190m
【解析】(1)由图读出电梯向上加速运动的最大加速度和减速运动的最大加速度大小,由牛顿第二定律求解最大拉力F1和最小拉力F2;(2)运用类比法可知,a﹣t图象与坐标轴所围的“面积”等于速度变化量,即可求出电梯匀速上升的速度,从而求高度.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目