题目内容
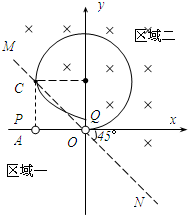
 在水平光滑的绝缘桌面内建立如图所示的直角坐标系,在虚线MON两侧区域分别称为区域一和区域二,其中一个区域内有匀强电场,另一个区域内有磁感应强度为B、方向垂直桌面的匀强磁场.现有一个质量为m、带电量为+q的小球P从坐标为(-L,0)的A点处由静止释放后,沿x轴运动至坐标原点O时,与另一与P球完全相同但不带电的静止小球Q发生碰撞并粘在一起,此后沿x轴正方向第一次经y轴进入区域二,经过一段时间,从坐标(-L,L)的C点回到区域一.若整个过程中,小球P带电量保持不变且P、Q两球可视为质点.
在水平光滑的绝缘桌面内建立如图所示的直角坐标系,在虚线MON两侧区域分别称为区域一和区域二,其中一个区域内有匀强电场,另一个区域内有磁感应强度为B、方向垂直桌面的匀强磁场.现有一个质量为m、带电量为+q的小球P从坐标为(-L,0)的A点处由静止释放后,沿x轴运动至坐标原点O时,与另一与P球完全相同但不带电的静止小球Q发生碰撞并粘在一起,此后沿x轴正方向第一次经y轴进入区域二,经过一段时间,从坐标(-L,L)的C点回到区域一.若整个过程中,小球P带电量保持不变且P、Q两球可视为质点.(1)指出哪个区域是电场、哪个区域是磁场以及电场和磁场的方向;
(2)求电场强度的大小;
(3)求小球P、Q第三次经过y轴的位置.
分析:(1)带电量为+q的小球P由A静止释放到O的运动可知区域一是电场,区域二为磁场;由运动方向可判断电场和磁场的方向.
(2)带电量为+q的小球在区域一中做匀加速直线运动,由动能定理可求得到达O点时的速度表达式;P、Q两球碰撞过程,由动量守恒定律可求得碰后速度的表达式;
P、Q球在磁场中一起做速率为v的匀速圆周运动,由几何关系求出轨迹半径,由牛顿第二定律求得速度,联立即可求得电场强度的大小.
(3)小球P、Q从C点回到区域一再到第三次经过y轴的过程中做类平抛运动,在电场方向上做初速度为零的匀加速直线运动,在垂直于电场的方向上做匀速直线运动,应用平抛运动的知识可求解.
(2)带电量为+q的小球在区域一中做匀加速直线运动,由动能定理可求得到达O点时的速度表达式;P、Q两球碰撞过程,由动量守恒定律可求得碰后速度的表达式;
P、Q球在磁场中一起做速率为v的匀速圆周运动,由几何关系求出轨迹半径,由牛顿第二定律求得速度,联立即可求得电场强度的大小.
(3)小球P、Q从C点回到区域一再到第三次经过y轴的过程中做类平抛运动,在电场方向上做初速度为零的匀加速直线运动,在垂直于电场的方向上做匀速直线运动,应用平抛运动的知识可求解.
解答:解:(1)区域一是方向与x轴正方向平行的匀强电场;区域二是方向垂直纸面向里的匀强磁场;
(2)小球的运动轨迹如图所示.
小球P从A运动到O点与小球Q碰撞前,设其速度为v0,由动能定理有:qEL=
m
①
P、Q两球碰撞过程,由动量守恒定律有:mv0=2mv ②
P、Q球在磁场中一起做速率为v的匀速圆周运动,由几何关系可知轨迹半径:
R=L ③
由牛顿第二定律有:qvB=2m
④
联立①②③④式解得,v=
,E=
⑤
(3)小球P、Q从C点回到区域一再到第三次经过y轴的过程中做类平抛运动,设此过程中小球P、Q未通过MON界线,沿y轴方向的位移为y,有:a=
⑥
L=
at2 ⑦
y=vt ⑧
联立⑤⑥⑦⑧式解得:y=
L
即小球P、Q第三次经过y轴在坐标原点O下方的位置是:y1=-(
L-L)=(1-
)L
答:
(1)区域一是方向与x轴正方向平行的匀强电场;区域二是方向垂直纸面向里的匀强磁场;
(2)电场强度的大小为
;
(3)小球P、Q第三次经过y轴的位置为(1-
)L.
(2)小球的运动轨迹如图所示.

小球P从A运动到O点与小球Q碰撞前,设其速度为v0,由动能定理有:qEL=
| 1 |
| 2 |
| v | 2 0 |
P、Q两球碰撞过程,由动量守恒定律有:mv0=2mv ②
P、Q球在磁场中一起做速率为v的匀速圆周运动,由几何关系可知轨迹半径:
R=L ③
由牛顿第二定律有:qvB=2m
| v2 |
| R |
联立①②③④式解得,v=
| qBL |
| 2m |
| qB2L |
| 2m |
(3)小球P、Q从C点回到区域一再到第三次经过y轴的过程中做类平抛运动,设此过程中小球P、Q未通过MON界线,沿y轴方向的位移为y,有:a=
| qE |
| 2m |
L=
| 1 |
| 2 |
y=vt ⑧
联立⑤⑥⑦⑧式解得:y=
| 2 |
即小球P、Q第三次经过y轴在坐标原点O下方的位置是:y1=-(
| 2 |
| 2 |
答:
(1)区域一是方向与x轴正方向平行的匀强电场;区域二是方向垂直纸面向里的匀强磁场;
(2)电场强度的大小为
| qB2L |
| 2m |
(3)小球P、Q第三次经过y轴的位置为(1-
| 2 |
点评:粒子进入有边界的磁场,由于边界条件的不同,而出现涉及临界状态的临界问题,可以根据边界条件确定粒子的轨迹、半径、在磁场中的运动时间等.解决此类问题常用的方法:画图→动态分析→找轨迹.

练习册系列答案
相关题目
 (2011?兴宁区模拟)在水平光滑的绝缘桌面内建立如图所示的直角坐标系,将第Ⅰ、Ⅱ象限称为区域一,第Ⅲ、Ⅳ象限称为区域二,其中一个区域内只有匀强电场,另一个区域内只有大小为2×10-2T、方向垂直桌面的匀强磁场.把一个荷质比为
(2011?兴宁区模拟)在水平光滑的绝缘桌面内建立如图所示的直角坐标系,将第Ⅰ、Ⅱ象限称为区域一,第Ⅲ、Ⅳ象限称为区域二,其中一个区域内只有匀强电场,另一个区域内只有大小为2×10-2T、方向垂直桌面的匀强磁场.把一个荷质比为 (2011?中山市三模)在水平光滑的绝缘桌面内建立如图所示的直角坐标系,第Ⅰ、Ⅱ象限有方向垂直桌面的匀强磁场.第Ⅲ、Ⅳ象限有大小为E的匀强电场,方向与x轴成45°.现把一个质量为m,电量为q的正电荷从坐标为(0,-
(2011?中山市三模)在水平光滑的绝缘桌面内建立如图所示的直角坐标系,第Ⅰ、Ⅱ象限有方向垂直桌面的匀强磁场.第Ⅲ、Ⅳ象限有大小为E的匀强电场,方向与x轴成45°.现把一个质量为m,电量为q的正电荷从坐标为(0,-
 b)的M点处由静止释放,电荷以一定的速度第一次经x轴进入磁场区域。经过一段时间,从坐标原点O再次回到电场区域。求:
b)的M点处由静止释放,电荷以一定的速度第一次经x轴进入磁场区域。经过一段时间,从坐标原点O再次回到电场区域。求: