题目内容
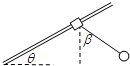（2013?徐汇区二模）如图所示，一固定杆与水平方向夹角为θ，将一质量为m1的滑块套在杆上，通过轻绳悬挂一个质量为m2的小球，杆与滑块之间的动摩擦因数为μ．若滑块与小球保持相对静止以相同的加速度a一起运动，此时绳子与竖直方向夹角为β，且θ＜β，则滑块的运动情况是（ ）分析：环与小球保持相对静止，并以相同的加速度a一起下滑，对整体进行受力分析求出加速度，采用隔离法，分析小球的受力，求出加速度，结合θ＜β分析即可判断．
解答：解：把环和球看做一个整体受力分析，沿斜面和垂直斜面建立直角坐标系得，
若速度方向向下，则
沿斜面方向：（m1+m2）gsinθ-f=（m1+m2）a 垂直斜面方向：FN=（m1+m2）gcosθ
摩擦力：f=μFN
联立可解得：a=gsinθ-μgcosθ，
对小球有：
a=gsinβ
所以gsinθ-μgcosθ=gsinβ
gsinθ-gsinβ=μgcosθ
因为θ＜β，所以gsinθ-gsinβ＜0，但μgcosθ＞0
所以假设不成立，即速度的方向一定向上．
由于加速度方向向下，所以物体沿杆减速上滑，故D正确．
故选D
若速度方向向下，则
沿斜面方向：（m1+m2）gsinθ-f=（m1+m2）a 垂直斜面方向：FN=（m1+m2）gcosθ
摩擦力：f=μFN
联立可解得：a=gsinθ-μgcosθ，
对小球有：
a=gsinβ
所以gsinθ-μgcosθ=gsinβ
gsinθ-gsinβ=μgcosθ
因为θ＜β，所以gsinθ-gsinβ＜0，但μgcosθ＞0
所以假设不成立，即速度的方向一定向上．
由于加速度方向向下，所以物体沿杆减速上滑，故D正确．
故选D
点评：分析多个物体的受力时，一般先用整体法来求得共同的加速度，再用隔离法分析单个物体的受力，求得物体的受力情况，本题就是典型的应用整体隔离法的题目．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
（2013?徐汇区二模）一列沿x轴正方向传播的简谐横波，波速为0.5m/s，在某时刻波形如图中实线所示，经过一段时间后波形如图中虚线所示，在这段时间内，图中P处的质点通过的路程可能是（ ）
（2013?徐汇区二模）在光滑绝缘的水平桌面上，存在着方向水平向右的匀强电场，电场线如图中实线所示．一带正电、初速度不为零的小球从桌面上的A点开始运动，到C点时，突然受到一个外加的水平恒力F作用而继续运动到B点，其运动轨迹如图中虚线所示，v表示小球经过C点时的速度．则（ ）
（2013?徐汇区二模）静电场方向平行于x轴，其电势φ随x的分布可简化为如图所示的折线．一质量为m、带电量为+q的粒子（不计重力），以初速度v0从O点（x=0）进入电场，沿x轴正方向运动．下列叙述正确的是（ ）
（2013?徐汇区二模）如图所示为α粒子散射实验装置，α粒子打到荧光屏上都会引起闪烁，若将带有荧光屏的显微镜分别放在图中A、B、C、D四处位置．则这四处位置在相等时间内统计的闪烁次数可能符合事实的是（ ）