题目内容
【题目】如图甲所示,两根平行光滑金属导轨相距L=lm,导轨平面水平面的夹角θ=30°,导轨的下端PQ间接有R=8Ω的电阻.相距x=6m的MN和PQ间存在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场,磁感应强度B时间t变化情况如图乙所示.将阻值r=2Ω导体棒ab垂直放在导轨上,使导体棒从t=0时由静止释放,t=1s时导体棒恰好运动到MN,开始匀速下滑.g取10m/s2.求:
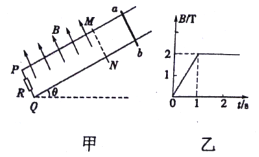
(1)01s内回路中的感应电动势;
(2)02s时间内导体棒所产生的热量。
【答案】(1)E1=12 V; (2)Q=4.88 J
【解析】试题分析:(1)在 0~1s内,磁场均匀变化,回路中产生恒定的感应电动势,由法拉第电磁感应定律求感应电动势;(2)0~2s时间内,根据焦耳定律求导体棒所产生的热量.
(1)0-1s内,磁场均匀变化,由法拉第电磁感应定律有:![]()
由图象得![]() ,且
,且![]()
代入解得:![]()
(2)在0~1s内回路中产生的感应电动势为![]()
根据闭合电路欧姆定律可得![]()
1s~2s内,导体棒从静止开始做匀加速运动,加速度 ![]()
t=1s末进入磁场区域的速度为![]()
导体棒切割磁感线产生的电动势 ![]()
根据闭合电路欧姆定律可得![]()
故0~2s时间内导体棒所产生的热量![]()
代入数据解得:Q=4.88J

练习册系列答案
相关题目